Способы соединения элементов САР

При решении задач анализа САР ее удобно представлять в виде структурной схемы (структурной динамической схемы), которая является графическим отображением математической модели системы. Имея такую модель и зная динамические характеристики отдельных звеньев, составляющих структурную схему, можно определить динамические характеристики САР.

Отдельные звенья на такой схеме условно обозначают в виде прямоугольников, внутри которых записывают выражения передаточной функции. Входные и выходные сигналы для каждого звена выражают в определенной форме, т.е. в виде изображений X(P) и Y(P). Устройство сравнения изображают в виде круга, разделенного на четыре сектора. Сектор, куда подается вычитаемая величина, обозначают знаком «-» или затушевывают.

Основными видами соединений звеньев являются: последовательное, параллельное и соединение с обратной связью (встречно-параллельное).

При последовательном соединении выход первого звена подсоединяется к входу последующего и т. д. (см. рис. 13.13). При таком соединении передаточные функции отдельных звеньев перемножаются. Произведение будет являться передаточной функцией всего соединения.

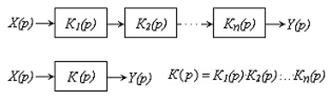
Рис. 13.13 – Последовательное соединение динамических звеньев

При параллельном соединении входы всех звеньев подсоединяются к источнику входного воздействия и образуют общий вход, а выходы соединяются вместе и являются общим выходом данного соединения (Рис. 13.14). Передаточной функцией всей цепи является алгебраическая сумма передаточных функций звеньев.

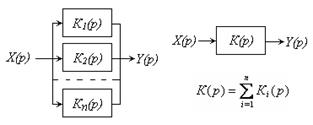
Рис. 13.14 – Параллельное соединение динамических звеньев

При соединении с обратной связью (ОС) выход одного звена через другое звено (звено обратной связи) связывается с его входом (рис. 13.15). При этом, если сигнал обратной связи вычитается из входного воздействия, обратная связь будет отрицательной (ООС), если складывается - положительной (ПОС).

Вид связи очень сильно влияет на вид характеристик и динамические свойства систем. Так при ООС повышается быстродействие системы и она становится более устойчивой к внешним воздействиям. Введение ПОС ухудшаются динамические свойства и устойчивость системы снижается.

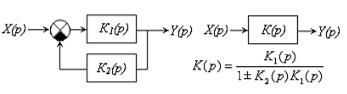
Рис. 13.15 – Соединение с обратной связью

В выражении для передаточной функции всего соединения (13.1) знак «+» ставится при ООС, а знак «-» соответствует ПОС, то есть

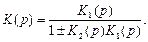(13.1)

Произведение К₂(р)·К₁(р), входящее в формулу (13.1), называется передаточной функцией разомкнутой системы и обозначается как К_Р(р), то есть

К_Р(р)=К₂(р)·К₁(р). (13.2)

Входящая в выражения (13.1) и (13.2) функция К₁(р) называется передаточной функцией прямой цепи.

Если К₂(р) = 1, т.е. выход звена К₁(р) cвязан непос-редственно с его входом, то передаточная функция системы упрощается. Тогда можно записать, что

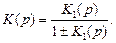(13.3)

Рассмотренные преобразования различных видов соеди-нений звеньев позволяют упростить структурную динами-ческую схему САР. Основное условие преобразования - неизменность динамических характеристик системы.

Устойчивость САР

Под устойчивостью системы понимают ее способность восстанавливать состояние равновесия после прекращения внешнего воздействия.

Для линейной системы связь между входным воздействием х(t) и выходной величиной y(t) описывается линейным дифференциальным уравнением (ЛДУ) n-го порядка:

a₀ y⁽ⁿ⁾(t) + a₁ y^(n-1)(t)+…+ a ^n-1y′(t)+a_n y(t) =

b₀ x^(m)(t)+b₁ x^(m-1)(t) + … + b _m-1x′(t)+b_m x(t) (13.4)

где a₀…a_n - коэффициенты, характеризующие параметры системы; b₀…b_m – коэффициенты, определяющие параметры входного воздействия, причем m ≤ n.

Решение ЛДУ представляется в виде двух составляющих – свободной y_св (t) и принужденной y_пр (t):

y(t)= y_св(t) + y_пр (t). (13.5)

Свободная составляющая характеризует свободное состо-яние системы, не зависящее от внешнего воздействия и опреде-ляемое только свойствами системы.

Устойчивость системы определяется ее поведением после прекращения входного воздействия, т.е. когда x(t)=0. В этом случае ЛДУ системы будет иметь вид:

a₀ y⁽ⁿ⁾(t) + a₁ y^(n-1)(t)+…+ a _n-1y′(t)+a_n y(t) = 0. (13.6)

Решение этого уравнения – свободная составляющая, характеризующая переходный процесс. Она будет иметь вид:

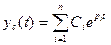, (13.7)

где С_i – постоянные интегрирования, определяемые пара-метрами системы; р_i - корни характеристического уравнения

a₀ pⁿ+a₁ p ^n-1+…+a _n-1 p+a_n=0, (13.8)

в котором оператор р заменяет операцию дифференцирования.

Из выражения (13.7) видно, что характер поведения системы, т.е. y_с(t) зависит от корней р_i уравнения (13.8).

В общем случае корни этого уравнения являются комплексно сопряженными, тоесть

р_i = α_i ± j β_i,

где α_i - действительная часть; β_i – мнимая часть.

Если корни р_i действительные (β_i = 0), тогда

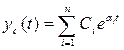. (13.9)

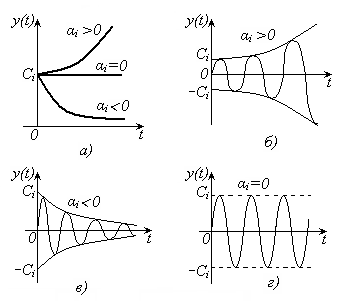
При этом, если для всех корней α_i < 0, то y_с(t) при t→ ∞ будет убывать. Переходный процесс будет затухающим и система будет устойчивой. Если хотя бы для одного из корней р_i > 0, то с течением времени (t → ∞) процесс y_с(t) будет нарастать, что свидетельствует о неустойчивости системы. Если хотя бы один корень р_i = 0, то система будет находиться на границе устойчивости. В случае, когда имеются комплексные корни, тогда в решении y_с(t) появятся соответствующие им слагаемые вида:

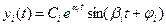, (13.10)

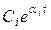где - частота колебания; - изменяющаяся во времени амплитуда; 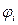- начальная фаза.

Характер этого колебания будет зависеть от :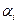

- при 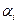>0 – колебание нарастает во времени;

- если 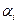<0 – затухающее колебание;

- при 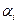=0 – незатухающее колебание с амплитудой 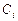(рис. 13.16 б, в, г).

Рис. 13.16 – Графики поведения системы: а) при 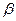= 0; б), в), г) – корни комплексно-сопряженные

Таким образом, линейная САР будет устойчивой, если действительные части всех корней ее характеристического уравнения будут отрицательными.

Однако нахождение корней характеристического уравнения для систем высокого порядка (n ≥ 3) чаще всего затруднительно. Существуют другие подходы для определения устойчивости системы, основанные на критериях устойчивости. При этом удобно пользоваться передаточной функцией замкнутой САР, которую получаем на основе ЛДУ, заменив символы производных оператором Лапласа р (см. п. 13.2). Тогда

(13.11)

Как видно из (13.11), характеристический полином находится в знаменателе выражения для .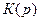

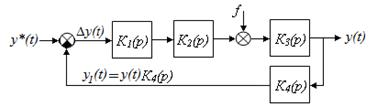
При анализе автоматических систем с замкнутой ОС (Рис. 13.17) применяют три вида передаточных функций.

1. Главная или основная передаточная функция К_y (p) по задающему воздействию. По определению

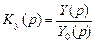. (13.12)

При этом полагают, что возмущающее воздействие f = 0.

Выражение для К_y(p) схемы САУ, изображенной на рис.13.17, получим, составив в операторной форме уравнение, связывающее величины Y(p) и Y₀(p):

[Y*(p) – Y(p) К₄(p)] К₁(p) К₂(p) К₃(p) = Y(p).

Рис. 13.17 – Структурная схема САУ: К1(p)… К4(p) – передаточные функции звеньев; y*(t) – задающее воздействие; y(t) – выходная величина; y1(t) – преобразованная выходная величина; ∆y(t) –рассогласование (∆y(t) = y*(t) – y1(t)); f – возмущающее воздействие

Раскрыв квадратные скобки, получим:

Y*(p) К₁(p) К₂(p) К₃(p) = Y(p) + Y(p) К₄(p) К₁(p) К₂(p) К₃(p) =

Y(p) [1 + К₄(p) К₁(p) К₂(p) К₃(p)].

Откуда следует, что

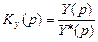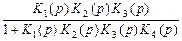= . (13.13)

Произведение К₁(p) К₂(p) К₃(p) К₄(p) = К_р(p), стоящее в знаменателе (13.13) – передаточная функция разомкнутой системы. Произведение в числителе К₁(p) К₂(p) К₃(p)= К_п(p) –функция прямой передачи. Тогда

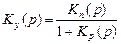. (13.14)

Звено с передаточной функцией К₄(p) является звеном обратной связи (см. рис. 13.17).

2. Передаточная функция по возмущающему воздействию К_f(p). Аналогичным образом при y₀ = 0, ее определяют, как

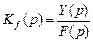. (13.15)

Операторное уравнение, связывающее величины Y(p) и F(p): [0 – Y(p) К₄(p)] К₁(p) К₂(p) К₃(p) + F(p) К₃(p) = Y(p). Из него получим:

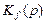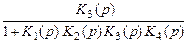= . (13.16)

3) Передаточная функция по рассогласованию К_∆(p). Приняв f = 0, найдем эту функцию, как

К_∆(p)= 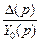. (13.17)

Из рис.13.17 видно, что Y(p)= ∆(p) К₁(p) К₂(p) К₃(p). Но ∆(p)= Y*(p) - Y(p) К₄(p)= Y*(p) - ∆(p) К₁(p) К₂(p) К₃(p) К₄(p).

Из последнего равенства получим, что ∆(p)+ ∆(p) К₁(p) К₂(p) К₃(p) К₄(p)= Y*(p). Далее: ∆(p)[1 + К₁(p) К₂(p) К₃(p) К₄(p)] = Y*(p). Выполнив последующие преобразования, получим:

К_ε(p)= 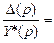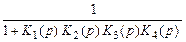. (13.18)

Сравнив выражения (13.13), (13.16) и (13.18) заметим, что знаменатель у них одинаков.