Звенья второго порядка

Для этих звеньев описывающее их дифференциальное уравнение имеет вид:

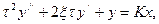
т.е. является линейным дифференциальным уравнением второго порядка. Коэффициенты τ и К имеют физический смысл постоянной времени и коэффициента передачи, аналогично как и для звеньев первого порядка. Коэффициент 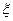характеризует затухание переходного процесса. Электрической моделью колебатель-ного звена второго порядка является колебательный контур (Рис.13.11). Примером консервативного звена также может быть маятник без потерь механической энергии (идеализированный вариант). Обычный маятник с потерями – пример колебательного звена, у которого 0< 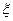<1.

Передаточная функция таких звеньев имеет вид:

.

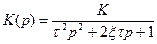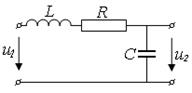
Рис.13.11 – Колебательный контур – модель колебательного звена (звено второго порядка)

При 0< 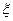<1 звено становится колебательным. Если 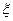<0, то колебательный процесс в переходной характеристике будет нарастать и такое звено называют неустойчивым колебательным звеном. При 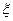≥1 переходной процесс переходит в затухающий (апериодический), и тогда получим апериодическое звено второго порядка. Если 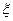= 0, колебания в переходной характеристике становятся незатухающими, и такое звено называют консервативным звеном.