Инерционные звенья второго порядка. При k = 1 передаточная функция звена: W(p) = .
При k = 1 передаточная функция звена: W(p) = 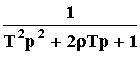 .
.
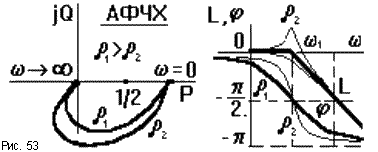
В виду сложности вывода выражений для частотных характеристик рассмотрим их без доказательства, они показаны на рис.53.
Асимптотическая ЛАЧХ колебательного звена до сопрягающей частоты 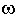 1 = 1/T1 совпадает с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном - 40 дб/дек. То есть высокие частоты колебательное звено "заваливает" сильнее, чем апериодическое звено.
1 = 1/T1 совпадает с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном - 40 дб/дек. То есть высокие частоты колебательное звено "заваливает" сильнее, чем апериодическое звено.
Реальная ЛАЧХ при 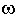
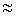
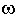 1 значительно отличается от асимптотической. Это отличие тем существенней, чем меньше коэффициент демпфирования
1 значительно отличается от асимптотической. Это отличие тем существенней, чем меньше коэффициент демпфирования 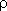 . Точную кривую можно построить, воспользовавшись кривыми отклонений, которые приводятся в справочниках. В предельном случае
. Точную кривую можно построить, воспользовавшись кривыми отклонений, которые приводятся в справочниках. В предельном случае 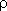 = 0 получаем консервативное звено, у которого при
= 0 получаем консервативное звено, у которого при 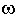
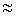
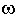 1 амплитуда выходных колебаний стремится к бесконечности (рис.54).
1 амплитуда выходных колебаний стремится к бесконечности (рис.54). 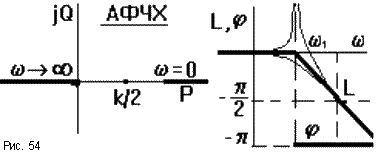
ЛФЧХ при малых частотах асимтотически стремится к нулю. При увеличении частоты до бесконечности выходной сигнал поворачивается по фазе относительно входного на угол, стремящийся в пределе к - 180о. ЛФЧХ можно построить с помощью шаблона, но для этого нужен набор шаблонов для разных коэффициентов демпфирования. При уменьшении коэффициента демпфирования АФЧХ приближается к оси абсцисс и в пределе у консервативного звена она вырождается в два луча по оси абсцисс, при этом фаза выходных колебаний скачком меняется от нуля до - 180о при переходе через сопрягающую частоту (рис.54).
Дата добавления: 2015-12-26; просмотров: 773;
