ОСОБЛИВОСТІ СИСТЕМАТИЧНОЇ СКЛАДОВОЇ ПОХИБОКИ

1)Присутність деяких ССП (особ­ливо при малих значеннях) важко визначити і

вони довгий час можуть бути невиявленими. Такі похибки виявляють шляхом вимірювання величини декількома незалежними методами з використовуванням первинних вимірювальних перетворювачів, побудованих із використанням різних фізичних явищ;

2) ССП завжди мають знак: «+» чи «-».

3) Якщо закон зміни систематичної похибки відомий, то її вплив легко врахувати у вигляді поправок, або усунути одним із методів автоматич­ного коригування;

4) єдиний спосіб виявлення ССП полягає в повірці нуля та чутливості ЗВ шляхом повторної його атестації по зразковим мірам.

Систематичні похибки, які змінюються по певному закону, виявляють

статис­тичними методами за допомогою спеціальних статистичних критеріїв.

У реальних умовах повністю усунути систематичну складову похибки (ССП) неможливо. Завжди залишаються не усунуті рештки, які треба враховувати, щоб оцінити їхні границі. Невиявлена ССП більш небезпечна, чим випадкова складова (ВСП). Якщо ВСП визиває розкид результатів вимiрювань, який називають

варіацією, то ССП визиває їх стійке спотворення, змiщення. У будь-якому випадку відсутність чи не значимість ССП, з метою нехтування, потрібно доказувати.

Так як причини, які приводять до появи ССП на протязі тривалого терміну часу змінюються за звичаєм по випадковому закону, то випадко­вою є також i систематична похибка. Тому, у загальному випадку, i систематична похибка описується з використанням теорії ймовірності та математичної статистики.

ВИЗНАЧЕННЯ СИСТЕМАТИЧНОЇ СКЛАДОВОЇ ПОХИБКИ (ССП)

Для визначення складових похибки вимірювання, як для випадку вимірювання

фізичної величини, так i для випадку повірки чи атестації засобів вимірювання, проводяться багаторазові (для першого випадку) вимірювання фізичної величини, випадку.

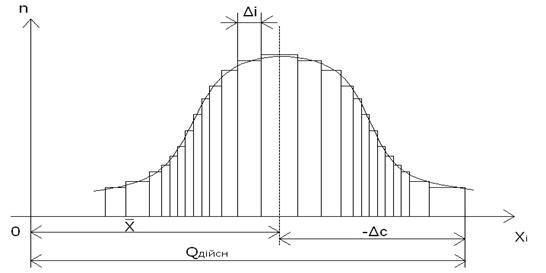
Рис. 3.2. Визначення систематичної складової похибки.

Отримавши ряд n результатів вимірювання Х1, Х2, Х3, ...Xn (загалом прийнято, щоб їх було не менше 20), для визначення систематичної складової похибки Δc, необхідно вирахувати середнє арифметичнеXср цього ряду результатів вимірювання за формулою:

Xср = 1/n * (X1+X2+X3+...+Xn) = 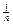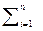Хi. (3.20)

Результати окремих вимірювань будуть згруповані біля Хср по ймовірносному

закону, як показано на рис 3.2.

Різниця Хср – Хоі = Δc, тобто, визначає ССП. Таким чином, відхилення середнього значення вимірюваної величини від її дійсного значення або зразкової міри, що подається на вхід ЗВ, характеризує ССП. Її ще інколи називають середньою арифметичною похибкою, або середнім арифметичним відхиленням. I, що дуже важливо, систематична похибка завжди має знак відхилення "+" чи "-".