ПОХИБКИ НЕПРЯМИХ ВИМІРЮВАНЬ.
Для посередніх вимірювань вихідними даними є формула зв’язку та результати прямих вимірювань величин – аргументів.
Якщо посередньо вимірювана величина У зв’язана з величинами – аргументами X1, X2,…, Хі,…, Xn деякою функціональною залежністю F, то, в загальному, можна записати:
У = F(X1, X2,…, Хі,…, Xn). (3.14)
Похибка непрямого вимірювання визначається похибками результатів вимірювання кожного виконаного прямого вимірювання.
Тому із урахуванням результатів проведених прямих вимірювань ввеличин-аргументів в певній точці характеристики перетворення, загальний результатУвим опосередкованого вимірювання має вигляд:
Увим = F(Х 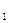 + ΔХ1, Х
+ ΔХ1, Х 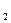 +ΔХ2, …, Х
+ΔХ2, …, Х  +ΔХn), (3.15)
+ΔХn), (3.15)
деХ 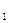 , Х
, Х 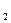 , … , Х
, … , Х  – істинні значення аргументів;
– істинні значення аргументів;
ΔХі –абсолютніпохибки вимірювань цих аргументів.
Абсолютна похибка ΔУ опосередкованого вимірювання дорівнює різниці:
ΔУ = F(Х 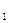 +ΔХ1, Х
+ΔХ1, Х 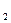 +ΔХ2,… , Х
+ΔХ2,… , Х 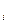 +ΔХ
+ΔХ 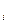 ,…, Х
,…, Х  +ΔХn) - F(Х
+ΔХn) - F(Х 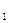 , Х
, Х 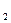 ,…, Х
,…, Х 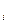 ,…, Х
,…, Х  ).
).
Але така формула непридатна для практичного використання.
Ураховуючи те, що значення похибки вимірювання завжди суттєво менше самої вимірюваної величини, функція F по залежності (1) може бути із високою точністю надана, в межах точки із координатами істинних значень аргументів, розкладом у ряд Тейлора, в якому враховані тільки складові першої степені:
У 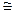 F(
F( 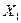 ,
, 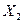 ,…,
,…, 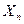 ) +
) + 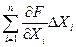 , (3.16)
, (3.16)
де 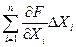
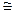 ΔУ – абсолютна похибка загального результату вимірювання;
ΔУ – абсолютна похибка загального результату вимірювання;
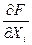 - перша частинна похідна від функції FпоХ
- перша частинна похідна від функції FпоХ 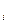 -томуаргументу;
-томуаргументу;
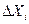 -відхилення результату вимірювання і-того аргументу від істинного його значення, тобто, абсолютна похибка вимірювання і-того аргументу.
-відхилення результату вимірювання і-того аргументу від істинного його значення, тобто, абсолютна похибка вимірювання і-того аргументу.
У реальних умовах ця формула дає дещо завищене значення похибкиΔУ,
так як при додаванні складових похибок можлива їхня часткова взаємна компе-
сація. Кращі результати дає середньоквадратичне підсумовування похибок:
ΔУ 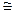
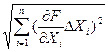 ,(3.17)
,(3.17)
де 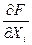
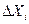 - часткова похибка результату опосередкованого вимірювання.
- часткова похибка результату опосередкованого вимірювання.
Відносна похибка опосередкованого вимірювання:
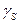 =
= 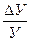 =
= 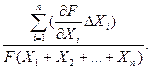 (3.18)
(3.18)
Якщо формула зв’язку є функцією одної змінної У = f(X), то абсолютна похибка ΔУ = | 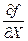 |ΔХ.Приклади таких функцій:
|ΔХ.Приклади таких функцій:
1. Якщо формула зв’язку має вигляд: У = Х 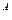 , то ΔУ
, то ΔУ 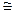 А* Х
А* Х 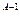 * ΔХ,а відносна похибка
* ΔХ,а відносна похибка 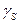 = ΔУ / У =
= ΔУ / У = 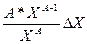 = А
= А 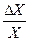 .
.
2. Якщо формула зв’язку має вигляд: У = 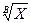 = Х
= Х 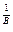 , то ΔУ
, то ΔУ 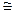
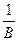 Х
Х 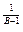 ΔХ,а відносна похибка
ΔХ,а відносна похибка 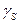 = ΔУ / У =
= ΔУ / У = 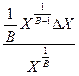 =
= 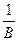
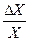 .
.
Якщо формула зв’язку є функцією алгебраїчної суми двох змінних Х 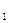 та Х
та Х 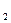 з коефіцієнтами a та b: У = аХ
з коефіцієнтами a та b: У = аХ 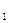 +вХ
+вХ 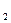 , то абсолютна похибка через середньоквадратичні підсумовування дорівнює: ΔУ =
, то абсолютна похибка через середньоквадратичні підсумовування дорівнює: ΔУ = 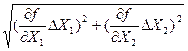 =
=
= 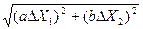 .
.
Якщо формула зв’язку є функцією добутку змінних Х 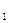 та Х
та Х 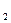 з коефіцієнтом К та показниками степені a та b (будь-які цілі або дробові, додатні або від’ємні числа): У = К Х
з коефіцієнтом К та показниками степені a та b (будь-які цілі або дробові, додатні або від’ємні числа): У = К Х 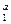 Х
Х 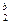 , то відносна похибка
, то відносна похибка
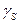 = ΔУ / У =
= ΔУ / У = 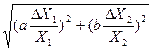 .
.
Якщо в результатах прямих вимірювань аргументів були використані надійні межі загальних похибок, то похибки опосередкованих вимірювань також відображають надійні межі загальних похибок цих результатів.
При багаторазових прямих вимірюваннях за найбільш ймовірне (істинне, дійсне) значення вимірюваної фізичної величини необхідно приймати середнє арифметичне результатів ряду вимірювань.
Відповідно при багаторазових непрямих (опосередкованих) вимірюваннях,
найбільш достовірний результат можна отримати, якщо у формулу зв’язку, будуть підставлені середні арифметичні значення цих аргументів.
У межах точки із координатами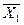 ,
, 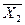 ,…,
,…, 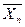 , достовірний результат вимірювання дорівнює:
, достовірний результат вимірювання дорівнює:
Увим 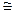 F(
F( 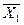 ,
, 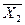 ,…,
,…, 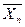 ) +
) + 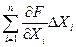 , (3.19)
, (3.19)
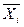 - середнє арифметичне (дійсне) значення величин – аргументів в даній точці характеристики перетворення, що вимірюються прямо.
- середнє арифметичне (дійсне) значення величин – аргументів в даній точці характеристики перетворення, що вимірюються прямо.
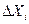 -відхилення результату вимірювання і-того аргументу від середнього
-відхилення результату вимірювання і-того аргументу від середнього
його значення 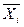 , яке приймається за дійсне (істинне).
, яке приймається за дійсне (істинне).
Отримання робочої формули для похибки непрямих вимірювань іноді пов’язане з громіздкими перетвореннями, які можна суттєво спростити в тих випадках, коли функцію зв’язку можна прологарифмувати.
Наприклад, достовірно визначити кількість тепла Q, що виділяється на опорі R при протіканні крізь нього струму Iза час t. Із фізики знаємо формулу зв’язку:
Q = I 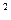 *R* t.
*R* t.
Логарифмуємо ліву та праву частини формули:
LnQ = 2 LnI + LnR + Lnt .
Далі обчислюємо першу похідну і підставляємо у формулу замість диференціалів відповідні кінцеві значення приростів 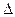 Q,
Q, 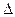 I,
I, 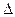 R,
R, 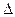 t та отримуємо абсолютну похибку:
t та отримуємо абсолютну похибку: 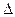 Q = 2
Q = 2 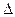 I +
I + 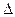 R +
R + 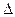 t.
t.
Відносна похибка: 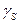 =
= 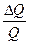 =
= 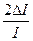 +
+ 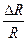 +
+ 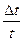 .
.
Якщо функцію зв’язку неможливо прологарифмувати безпосередньо, то її необхідно або перетворити до виду, необхідному для логарифмування, або вивести формулу похибки диференціюванням.
Дата добавления: 2016-01-18; просмотров: 5798;
