Статистическое распределение выборки

Разработка методов регистрации, описания и анализа статистических экспе­риментальных данных, полученных в результате наблюдения массовых случайных явлений, составляет предмет математической статистики.

Эти методы позволяют получать обоснованные выводы о параметрах или виде распределения случайных величин по совокупности наблюдений над ними – выборке.

Пусть проводится экспе­римент со случайной величиной 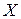, имеющей функцию распределения .

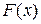Определение. Выборкой объема 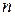из генеральной совокупности с функ­цией распределения 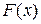называется последовательность 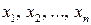наблюдае­мых значений случайной величины 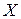, соответствующих 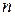независи­мым повторениям эксперимента.

Замечание. Выборку объема 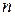можно определить как совокупность 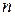слу­чайно отобранных объектов из некоторого множества объектов – генераль­ной совокупности.

Пусть в результате эксперимента получены значения изучаемой случай­ной величины 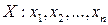(среди них могут быть повторяющиеся значения).

Определение. Вариационным рядом выборки 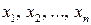называется способ ее записи, при котором элементы выборки упорядочиваются по величине, то есть записы­ваются в виде последовательности 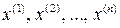, где .

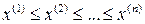Пусть в выборке объема 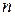число 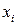встречается 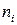раз .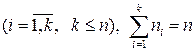

Определение. Числа 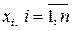называют вариантами. Число 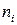называют частотой варианты 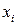. Число 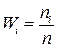называют относительной частотой варианты .

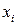Определение. Размахом выборки называется разность между максимальной и минимальной вариантой выборки .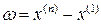

Определение. Статистическим распределением выборки (статистическим рядом) называется последовательность пар 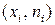или .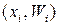

Обычно статистический ряд записывается в виде таблицы, первая строка которой содержит упорядоченные по величине варианты 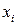, а вторая – их частоты (или относительные частоты).

Пример. Записать вариационный ряд и статистическое распределение выборки 4,3,3,1,2,2,5,4,4,3,5,5,6,6,4. Определить размах выборки.

Решение. Объем выборки 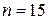. Упорядочив варианты по величине, получим вариационный ряд 1,2,2,3,3,3,4,4,4,4,5,5,5,6,6. Размах выборки .

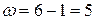Статистическое распределение выборки

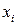
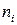
для контроля правильности записи находим: ;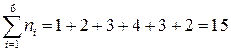

или

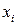
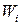
	1/15	2/15	3/15	4/15	1/15	2/15

для контроля записи находим: .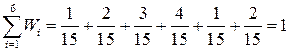

При большом объеме выборки ее элементы (варианты) объединяют в группы, представляя результаты опыта в виде группированного статистического ряда. Для этого интервал, содержащий все варианты выборки, разбивается на 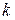частичных непересекающихся интервалов. Для упрощения вычислений частичные интервалы выбирают одинаковой длины 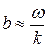. После того, как частичные интервалы выбраны, определяют частоты – количество 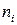вариант, попавших в 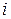-й интервал (варианта, совпадающая с верхней границей интервала, относится к последующему интервалу). Получающийся статистический ряд в верхней строке содержит середины 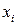интервалов группировки, а в нижней – частоты .

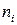В зависимости от объема выборки число интервалов группировки 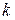берется от 6 до 20. Следует помнить, что группировка вносит погрешность в дальнейшие вычисления, которая растет с уменьшением числа интервалов.

Для наглядности представления полученных статистических экспериментальных данных весьма целесообразно наряду со статистическим распределением выборки давать графическое представление.

Определение. Полигоном частот (относительных частот) группированной выборки называется ломаная с вершинами в точках 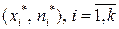(в точках ).

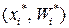Определение. Гистограммой частот (относительных частот) группированной выборки называется ступенчатая фигура, составленная из прямоугольников, построенных на частичных интервалах группировки, высоты которых равны .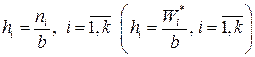

Отсюда следует, что площадь гистограммы равна объему выборки, а площадь гистограммы относительных частот - единице.

Пример. Представить выборку 55 наблюдений в виде группированного статистического ряда, используя 7 интервалов группировки. Построить полигон и гистограмму частот группированной выборки.

Выборка

Решение. Размах выборки 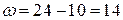, количество интервалов – 7. Длина интервала .

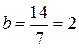Сформируем группированное статистическое распределение выборки

Номер интервала i
Границы интервала	10-12	12-14	14-16	16-18	18-20	20-22	22-24
Середина интервала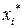
Частота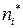
Относительная частота	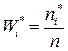0,0364	0,0727	0,1455	0,2182	0,2909	0,1818	0,0545

Полигон группированных относительных частот изображен на Рис. 7.

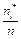
0.3 - .     0.2 - . 0.1 -     11 15 19 23 Рис. 7.

Гистограмма группированных частот представлена на Рис. 8.

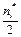8 -   6 -   4 -     2 -   12 16 20 24 Рис. 8.