Числовые характеристики случайного вектора

Определение.Точка с координатами 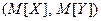называется математическим ожиданием случайного вектора 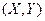или центром рассеивания.

Определение.Ковариацией двух случайных величин 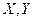называется математическое ожидание произведения их отклонений от соответствующих математических ожиданий: .

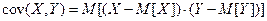Для ковариации верны соотношения:

1. ;

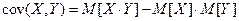2. .

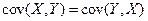Если случайные величины 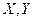независимы, то их ковариация равна нулю: 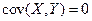. Если 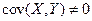, то случайные величины зависимы.

Определение.Коэффициентомкорреляции 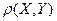случайных величин 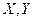называется отношение их ковариации к произведению средних квадратических отклонений этих величин: 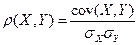. (Коэффициент корреляции есть нормированная ковариация).

Определение.Случайные величины 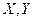, для которых 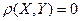, называются некоррелированными.

Коэффициент корреляции определяет степень линейной зависимости между 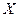и .

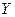Свойствакоэффициентакорреляции:

1) ;

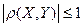2) если величины 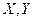независимы, то ;

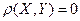3) если 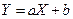, то .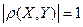

Таким образом, из независимости случайных величин вытекает их некоррелируемость, обратное неверно.

Определение.Условным математическим ожиданием случайной величины 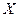при условии, что 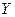приняла одно из своих возможных значений, называется действительное число, обозначаемое 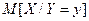и определяемое формулами:

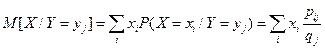- для дискретных величин;

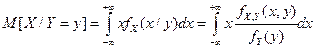- для непрерывных величин.

Определение.Для двух случайных величин 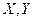регрессией 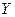на 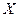называется условное математическое ожидание случайной величины 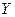, выраженное как функция от 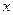: 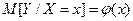. График этой функции называется кривой регрессии.

Функция регрессии может использоваться для предсказания значения случайной величины 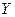по фиксированному значению случайной величины .

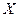Если 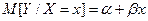, то говорят о линейной регрессии 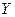на 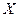, графиком линейной регрессии является прямая.