Нормальное распределение. Определение.Нормальным распределением (или распределением Гаусса) называется распределение случайной величины

Определение.Нормальным распределением (или распределением Гаусса) называется распределение случайной величины, плотность которого равна: .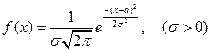

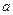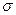Параметры и нормально распределенной случайной величины 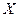имеют следующий смысл: , .

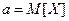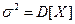Функция распределения этой случайной величины есть: 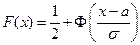, где 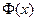- функция Лапласа: .

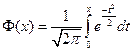Функция Лапласа является нечетной, ее значения приведены в специальных таблицах.

Вероятность попадания нормально распределенной случайной величины 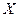в интервал 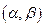определяется формулой

.

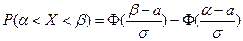Вероятность выполнения неравенства 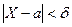, т.е. вероятность того, что случайная величина отклонится от своего математического ожидания не больше, чем на величину 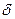, для нормально распределенной случайной величины 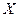есть: .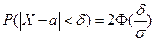

Пример.Найти вероятность попадания в интервал 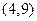нормально распределенной случайной величины 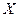, для которой математическое ожидание 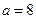, среднее квадратическое отклонение .

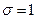Решение. Применим формулу: 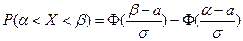; в данном случае она примет вид: .

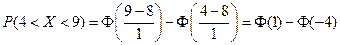Функция Лапласа является нечетной, поэтому

.

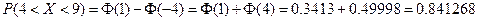Значения 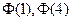найдены по таблице значений функции Лапласа (приложение 1).