Эмпирическая функция распределения

Пусть проведен эксперимент, связанный со случайной величиной Х и получена группированная выборка объема n из генеральной совокупности с функцией распределения 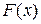( группированный статистический ряд):

			. . .
			. . .

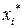
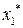
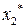
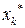
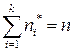
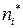
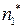
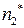
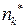
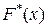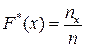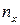Определение. Эмпирической функцией распределения (функцией распределения выборки) называется числовая функция , определяемая соотношением: , где - число опытов, в которых наблюдали значения случайной величины Х меньшие х, т.е. .

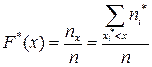Замечание. В отличие от эмпирической функции распределения 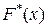, функцию распределения генеральной совокупности 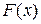называют теоретической функцией распределения. Отметим, что если значение теоретической функции 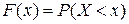для каждого значения аргумента х равно вероятности осуществления события, состоящего в том, что случайная величина Х приняла значение меньшее х, то значение эмпирической функции распределения 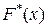равно частоте осуществления того же события.

Свойства эмпирической функции распределения вытекают из ее определения:

1) Значения 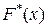принадлежат интервалу , .

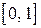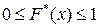2) Функция 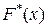- неубывающая функция, то есть если 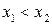, то .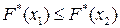

3) Если 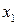- наименьшая варианта, то при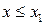 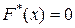. Если 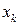- наибольшая варианта, то при .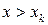

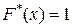Пример. По данным примера из пункта 4.1.1. построить эмпирическую функцию распределения.

Решение.

Рассмотрим группированное статистическое распределение выборки:

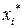
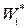
	0,0364	0,0727	0,1455	0,2182	0,2909	0,1818	0,0545

Вычислим значения 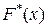, если 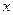попадает в каждый из интервалов группировки (для этого складываем относительные частоты всех предыдущих интервалов):

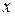
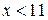
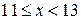
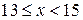
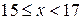
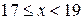
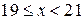
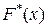
		0,0364	0,1091	0,2546	0,4728	0,7637

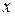
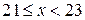
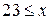
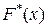
	0,9455	1,0000

Построим график этой таблично заданной функции, Рис. 9 (стрелками показано, какому из отрезков принадлежит концевая точка):

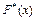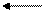1- - - - - 0,5- - - - - х 10 12 14 16 18 20 22 24

Рис. 9