Метод максимального правдоподобия
Для нахождения точечных оценок параметров распределения можно использовать метод максимального правдоподобия. Этот метод основан на следующем интуитивном представлении: в большинстве случаев в эксперименте наблюдается именно то значение случайной величины Х, при котором плотность вероятности 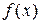 близка к максимальному значению.
близка к максимальному значению.
Согласно методу максимального правдоподобия для нахождения оценки параметра 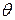 на основании выборки
на основании выборки 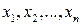 :
:
1) составляют функцию правдоподобия:
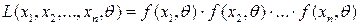 ,
,
(это функция аргумента 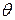 и элементов выборки,
и элементов выборки, 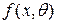 - плотность распределения случайной величины Х, содержащая неизвестный параметр,
- плотность распределения случайной величины Х, содержащая неизвестный параметр,  - значение плотности при
- значение плотности при 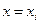 );
);
2) находят то значение 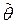 , при котором функция правдоподобия принимает максимальное значение:
, при котором функция правдоподобия принимает максимальное значение: 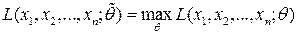 . Для этого находят точку максимума функции
. Для этого находят точку максимума функции 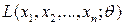 :
:
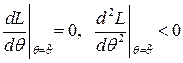 .
.
Иногда для упрощения вычислений удобно рассматривать логарифм функции правдоподобия.
3) в качестве точечной оценки параметра 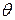 принимают найденное значение
принимают найденное значение 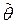 .
.
Определение.Оценку 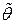 называют оценкой наибольшего (максимального) правдоподобия.
называют оценкой наибольшего (максимального) правдоподобия.
Оценки параметров, полученные по методу максимального правдоподобия, асимптотически нормально распределены и для некоторых законов распределения генеральной совокупности имеют минимальную дисперсию.
Пример. Найти оценку параметра 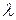 показательного распределения
показательного распределения 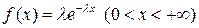 , если в результате испытаний величины Х, распределенной по показательному закону, получены значения
, если в результате испытаний величины Х, распределенной по показательному закону, получены значения 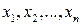 .
.
Решение. Составим функцию правдоподобия:
 .
.
Для упрощения вычислений найдем: 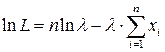 , и его точку максимума:
, и его точку максимума:
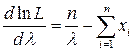 ,
, 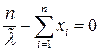 ,
, 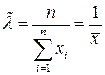 (здесь
(здесь 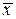 - выброчное среднее).
- выброчное среднее).
Так как 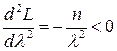 , то функция правдоподобия принимает максимальное значение при
, то функция правдоподобия принимает максимальное значение при 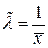 , значит
, значит 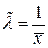 - искомая оценка параметра
- искомая оценка параметра 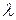 .
.
Дата добавления: 2016-01-09; просмотров: 2160;
