Контрольная работа № 8. Задания
1. Решить задачу (таблица 6).
2. Решить задачу с использованием формулы Бернулли (таблица 7).
3. По заданной плотности распределения найти требуемые величины (табл. 8).
4. По сгруппированным данным построить гистограмму относительных частот
(таблица 9).
5.Проверить нулевую гипотезу о том, что заданное значение 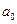 является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема
является математическим ожиданием нормально распределенной случайной величины при 5% уровне значимости для двусторонней критической области, если в результате обработки выборки объема 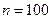 получено выборочное среднее
получено выборочное среднее 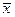 , а несмещенное квадратичное отклонение равно
, а несмещенное квадратичное отклонение равно 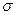 (таблица 10).
(таблица 10).
6. Найти выборочное уравнение линейной регрессии 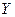 на
на 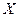 на основании корреляционной таблицы (таблица 11).
на основании корреляционной таблицы (таблица 11).
6.1. Пример выполнения контрольной работы № 2. Вариант № 0.
1.В урне 15 шаров: 5 белых и 10 черных. Какова вероятность того, что извлекли два разноцветных шара?
Решение. Эксперимент состоит в извлечении двух шаров из пятнадцати. Выбор осуществляется без возвращения, порядок извлеченных шаров не играет роли. Элементарным исходом является пара объектов вида: номер шара и его цвет, например: (первый белый, третий черный). Количество таких исходов 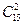 . Рассмотрим среди них исходы, благоприятствующие событию А={извлекли два разноцветных шара}. Количество способов выбрать один белый шар из 5 равно
. Рассмотрим среди них исходы, благоприятствующие событию А={извлекли два разноцветных шара}. Количество способов выбрать один белый шар из 5 равно 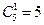 , количество способов выбрать один черный шар из 10 равно
, количество способов выбрать один черный шар из 10 равно 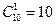 . Таким образом, количество благоприятствующих исходов
. Таким образом, количество благоприятствующих исходов 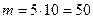 . Воспользуемся формулой классической вероятности:
. Воспользуемся формулой классической вероятности: 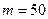 , а
, а 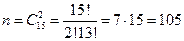 . Следовательно,
. Следовательно, 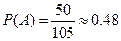 .
.
Ответ. 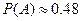 .
.
2.Вероятность того, что расход электроэнергии в течение одних суток не превысит установленной нормы, равна 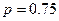 . Найти вероятность того, что в ближайшую неделю расход электроэнергии не превысит нормы в течении 4 суток.
. Найти вероятность того, что в ближайшую неделю расход электроэнергии не превысит нормы в течении 4 суток.
Решение. Эксперимент состоит в том, что в течение 7 дней наблюдают за расходом электроэнергии. Вероятность нормального расхода электроэнергии в продолжении каждых суток в неделю постоянна и равна 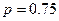 . Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна
. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна 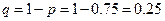 . Искомое событие: А={ровно 4 раза в течении 7 дней расход электроэнергии будет нормальным}.
. Искомое событие: А={ровно 4 раза в течении 7 дней расход электроэнергии будет нормальным}.
Используя формулу Бернулли, получаем:
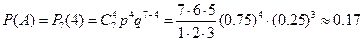 . Ответ.
. Ответ. 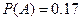 .
.
3. Задана плотность распределения непрерывной случайной величины 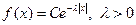 - параметр распределения.
- параметр распределения.
Найти нормировочную константу С, функцию распределения F(x), математическое ожидание M[X], дисперсию D[X].
Решение.
А) Константу С находим из свойства нормировки плотности распределения: 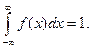
В данном случае, т.к. плотность содержит переменную под знаком модуля, то интеграл разбивается на два интеграла:
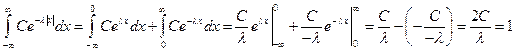 .
.
Отсюда 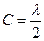 .
.
Б) Плотность распределения и функция распределения связаны соотношением: 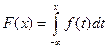 .
.
Запишем плотность распределения следующим образом: 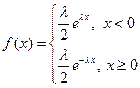 . Функцию распределения будем искать, используя эти промежутки.
. Функцию распределения будем искать, используя эти промежутки.
При 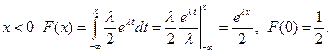
При 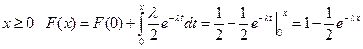 .
.
Таким образом, функция распределения имеет вид:
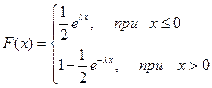 .
.
В) Математическое ожидание непрерывной случайной величины равно:
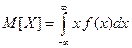 . В рассматриваемом случае:
. В рассматриваемом случае:
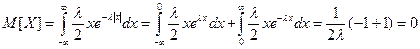 (при вычислении интегралов использовалась формула интегрирования по частям).
(при вычислении интегралов использовалась формула интегрирования по частям).
Дисперсию случайной величины вычислим по формуле: 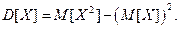 Так как математическое ожидание равно 0, то дисперсия будет равна
Так как математическое ожидание равно 0, то дисперсия будет равна 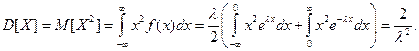
Ответ: Для непрерывной случайной величины Х: нормировочная константа равна 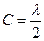 , функция распределения
, функция распределения 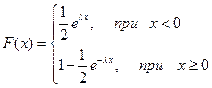 , математическое ожидание
, математическое ожидание 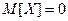 , дисперсия
, дисперсия 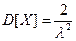 .
.
4.Задан интервальный вариационный ряд. Рассчитать и построить гистограмму относительных частот по сгруппированным данным, здесь 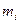 - частота попадания вариант в промежуток (
- частота попадания вариант в промежуток ( 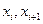 ).
).
| № | 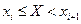
| mi |
| 2 - 4 | 5 | |
| 4 - 6 | 8 | |
| 6 - 8 | 16 | |
| 8 - 10 | 12 | |
| 10 - 12 | 9 |
Решение.
Для построения гистограммы надо рассчитать относительные частоты. Объем выборки: n=5+8+16+12+9=50. Длина интервалов: h=2. Относительные частоты определяются по формуле: 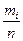 . Их значения равны для соответствующих интервалов: 0.1; 0.16; 0.32; 0.24; 0.18. Интервальный вариационный ряд графически изображают с помощью гистограммы. Для ее построения на оси х откладывают отрезки частичных интервалов варьирования, на них строят прямоугольники высотой, равной относительной частоте. Для заданного примера гистограмма приведена на Рис. 12 .
. Их значения равны для соответствующих интервалов: 0.1; 0.16; 0.32; 0.24; 0.18. Интервальный вариационный ряд графически изображают с помощью гистограммы. Для ее построения на оси х откладывают отрезки частичных интервалов варьирования, на них строят прямоугольники высотой, равной относительной частоте. Для заданного примера гистограмма приведена на Рис. 12 .
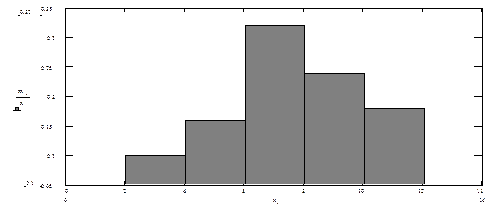
Рис.12
5. Из нормальной генеральнойсовокупности с параметрами 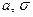 с известным средним квадратическим отклонением
с известным средним квадратическим отклонением 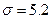 извлечена выборка объема
извлечена выборка объема 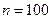 и по ней найдена выборочная средняя
и по ней найдена выборочная средняя 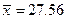 . Требуется при уровне значимости
. Требуется при уровне значимости 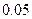 по сгруппированным данным проверить нулевую гипотезу
по сгруппированным данным проверить нулевую гипотезу 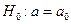
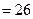 при конкурирующей гипотезе
при конкурирующей гипотезе 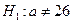 .
.
Решение. Данная задача относится к задачам проверки статистических гипотез, а именно, производитсясравнение выборочной средней с гипотетической генеральной средней для нормальной совокупности, если дисперсия генеральной совокупности известна.
Для того, чтобы при заданном уровне значимости 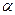 проверить нулевую гипотезу
проверить нулевую гипотезу 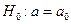 о равенстве генеральной средней
о равенстве генеральной средней 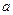 нормальной совокупности с известной дисперсией
нормальной совокупности с известной дисперсией 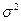 гипотетическому (предполагаемому) значению
гипотетическому (предполагаемому) значению 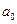 , при конкурирующей гипотезе
, при конкурирующей гипотезе 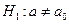 , надо:
, надо:
- вычислить наблюдаемое значение критерия 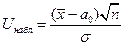 ,
,
- по таблице значений функции Лапласа найти критическую точку 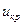 двусторонней критической области из равенства
двусторонней критической области из равенства 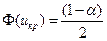 .
.
Если 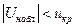 - нулевую гипотезу принимают, если
- нулевую гипотезу принимают, если 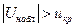 - нулевую гипотезу отвергают. Найдем наблюдаемое значение критерия:
- нулевую гипотезу отвергают. Найдем наблюдаемое значение критерия:
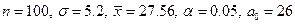 ;
; 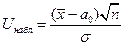
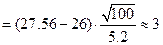 .
.
По условию, конкурирующая гипотеза имеет вид 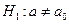 , поэтому критическая область – двусторонняя.
, поэтому критическая область – двусторонняя.
Найдем критическую точку из равенства 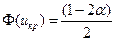
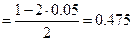 . По таблице функции Лапласа находим
. По таблице функции Лапласа находим 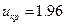 . Так как
. Так как 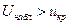 - нулевую гипотезу отвергаем, т.е выборочная и гипотетическая средние различаются значимо.
- нулевую гипотезу отвергаем, т.е выборочная и гипотетическая средние различаются значимо.
Ответ. Гипотеза о том, что параметр 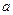 нормальной генеральной совокупности равен 26, отвергается, т.к. не соответствует выборочным данным.
нормальной генеральной совокупности равен 26, отвергается, т.к. не соответствует выборочным данным.
5.Найти выборочное уравнение линейной регрессии 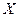 на
на 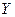 по данным корреляционной таблицы.
по данным корреляционной таблицы.
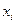 
| ||||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - |
Решение. В том случае, когда варианты парной выборки встречаются по нескольку раз, причем с одним значением варианты 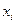 может встретиться несколько вариант
может встретиться несколько вариант 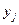 , их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечают частоту
, их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечают частоту 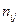 выбора соответствующей пары (
выбора соответствующей пары ( 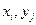 ). Частоты вариант находят как суммы по строкам и столбцам:
). Частоты вариант находят как суммы по строкам и столбцам: 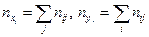 . Очевидно, что
. Очевидно, что 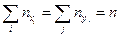 - объем выборки.
- объем выборки.
Выборочное уравнение прямой линии регрессии 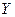 на
на 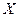 имеет вид
имеет вид 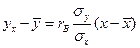 ,
,
где 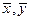 - выборочные средние для случайных величин
- выборочные средние для случайных величин 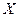 и
и 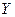 ;
; 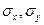 - выборочные средние квадратические отклонения;
- выборочные средние квадратические отклонения; 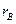 - выборочный коэффициент корреляции, причем
- выборочный коэффициент корреляции, причем 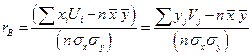 ,
, 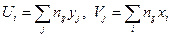 .
.
Выборочное уравнение прямой линии регрессии 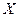 на
на 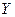 имеет вид
имеет вид 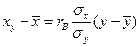 .
.
Если данные наблюдений над признаками 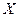 и
и 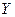 заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:
заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам: 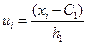 ,
, 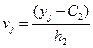 , где
, где 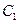 - «ложный нуль» вариант
- «ложный нуль» вариант 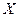 ( новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту);
( новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного нуля варианту, имеющую наибольшую частоту); 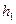 - шаг, т.е. разность между двумя соседними вариантами
- шаг, т.е. разность между двумя соседними вариантами 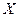 ;
; 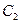 - ложный путь вариант
- ложный путь вариант 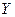 ;
; 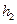 - шаг вариант
- шаг вариант 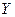 .
.
В этом случае выборочный коэффициент корреляции 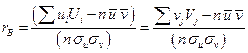 ,
, 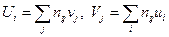 .
.
Величины 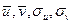 могут быть найдены по формулам:
могут быть найдены по формулам: 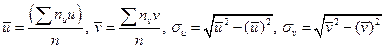 .
.
По этим значениям можно определить входящие в уравнения регрессии величины по формулам: 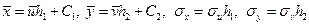 .
.
В заданной корелляционной таблице выберем в качестве ложных нулей 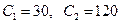 . Шаг варианты
. Шаг варианты 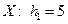 , шаг варианты
, шаг варианты 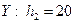 . Для упрощения расчетов введем условные варианты
. Для упрощения расчетов введем условные варианты 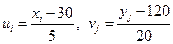 и составим преобразованную корреляционную таблицу с условными вариантами, в которую внесем значения
и составим преобразованную корреляционную таблицу с условными вариантами, в которую внесем значения 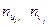 :
:
 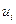
| -3 | -2 | -1 | 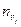
| |||
| -1 | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | - | ||||||
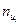
| 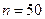
|
Затем составим новую таблицу, в которую внесем найденные значения 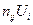 в правый верхний угол заполненной клетки и
в правый верхний угол заполненной клетки и 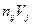 в левый нижний угол, по центру остается частота. После этого суммируем верхние значения по строкам для получения значений
в левый нижний угол, по центру остается частота. После этого суммируем верхние значения по строкам для получения значений 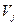 и нижние значения по столбцам для
и нижние значения по столбцам для 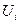 и подсчитаем величины
и подсчитаем величины 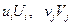 :
:
 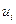
| -3 | -2 | -1 | 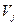
| 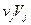
| |||
| -1 | -6 -2 | -2 -1 | - | -7 | - | - | -8 | |
| -12 | - | -2 | - | - | -8 | |||
| - | -10 | - | -1 | -1 | ||||
| - | - | -3 | ||||||
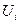
| -2 | - | 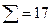
| |||||
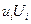
| -8 | -6 | 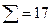
| - |
Проверяем суммы 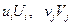 , получаем
, получаем 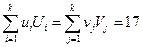 .
.
Находим 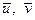 (умножаем значение варианты на сумму ее частот и находим среднее арифметическое этих величин):
(умножаем значение варианты на сумму ее частот и находим среднее арифметическое этих величин):
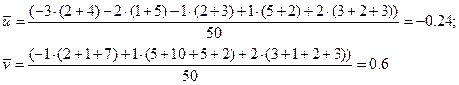
Находим 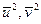 :
:
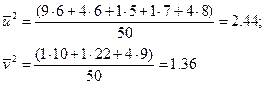
Определяем 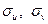 :
:
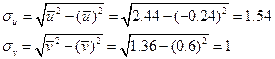
Вычисляем выборочный коэффициент корреляции 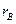 :
:
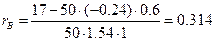
Осуществим переход к исходным вариантам:
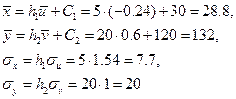
Находим уравнение линии регрессии 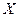 на
на 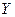 :
: 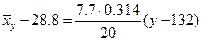 или
или 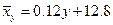 . Аналогично, уравнение линии регрессии
. Аналогично, уравнение линии регрессии 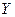 на
на 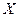 :
:
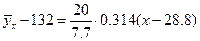 или
или 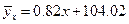 .
.
Ответ. Линии регрессии имеют вид: 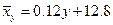 и
и 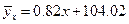 .
.
Дата добавления: 2016-01-09; просмотров: 4496;
