Вероятность отсутствия дефицита Р(x) и
значение коэффициента хр для нормального закона распределения
| Уровень обслуживания с вероятностью отсутствия дефицита Р(x) | Коэффициент хр |
| 0,65 | 0,385 |
| 0,7 | 0,525 |
| 0,75 | 0,675 |
| 0,8 | 0,842 |
| 0,85 | 1,037 |
| 0,9 | 1,28 |
| 0,92 | 1,405 |
| 0,94 | 1,555 |
| 0,95 | 1,645 |
| 0,96 | 1,75 |
| 0,98 | 2,05 |
| 0,99 | 2,3 |
| 0,999 | 3,1 |
Пример 3.1:
Для исходных данных, представленных в таблице 3.2 необходимо произвести расчет текущего и страхового запасов с использованием статистических формул (3.1) – (3.9).
Коэффициент хp в расчетах примем равным 2, то есть соответствующим вероятности отсутствия дефицита 0,98 (см. табл. 3.1).
Для расчета значения среднесуточного расхода материальных ресурсов в рассматриваемом примере воспользуемся формулой (3.10).
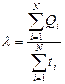, (3.10)
где Qi – величина i-й поставки, ед.;
ti – значение интервала времени между поставками (до следующей поставки), дней.
Таблица 3.2.
Исходные данные для расчетов
| Интервал времени до следующей поставки ti, дней. | Объем поставки Qi, ед. |
Результаты расчетов приведены в табл. 3.3.
Таблица 3.3
Результаты расчетов параметров текущего и страхового запасов через интервалы времени между поставками
| № | ti, дн. | Qi, ед. | tiQi |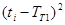 
| 
| 
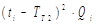
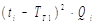
| tj1≥TТ1 | tj2≥TТ2 | tj1Qj1 | tj2Qj2 | Qj1 | Qj2 |
| Сумма | ||||||||||||
| N | хp | λ | ||||||||||
| TТ1 (ф. 3.1) | Tc1 (ф. 3.5) | 4,1 | Sc1 | 16,4 | ||||||||
| TТ2 (ф. 3.2) | Tc2 (ф. 3.6) | Sc2 | ||||||||||
| λ | Tc3 (ф. 3.7) | 4,3 | Sc3 | 17,2 | ||||||||
| SТ1 (ф. 3.3) | Tc4 (ф. 3.8) | 3,3 | Sc4 | 13,2 | ||||||||
| SТ2 (ф. 3.4) | Tc5 (ф. 3.9) | 2,2 | Sc5 | 8,8 |
Дата добавления: 2016-01-07; просмотров: 1123;