Формула Мора для вычисления прогиба
Пусть необходимо найти прогиб точки В, т.е. перемещение vB.(рис.16.2)

Рис. 16.2.
Для решения задачи используем применим закон сохранения энергии в варианте принципа возможных перемещений. В качестве возможных выберем прогиб  (здесь и далее величины, характеризующие основную задачу будут снабжаться индексом q).
(здесь и далее величины, характеризующие основную задачу будут снабжаться индексом q).
Рассмотрим фиктивную задачу (рис.16.3)
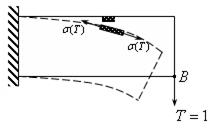
Рис. 16.3.
Вычислим работу силы  на перемещении
на перемещении 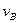 :
:
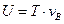 .
.
Согласно закона сохранения энергии эта работа должна равняться работе внутренних сил. Подсчитаем её.
Рассмотрим рис.16.2 и рис.16.3. Выделим малый элемент балки (он зачернен на рис 16.2 и рис.16.3). Он удлиняется на величину  .
.

Рис. 16.4.
Рассмотрим этот же малый элемент под действием напряжений растяжения 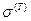 (здесь и далее величины, характеризующие фиктивную задачу, будут снабжаться индексом Т), которые возникают, под действием силы Т. Вычислим
(здесь и далее величины, характеризующие фиктивную задачу, будут снабжаться индексом Т), которые возникают, под действием силы Т. Вычислим  - работу этих напряжений на перемещении
- работу этих напряжений на перемещении  :
:

Согласно определению:
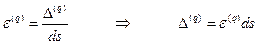
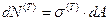
Таким образом,

Здесь  – объем малого элемента.
– объем малого элемента.
Работа по удлинению всех элементов балки будет:
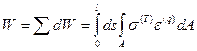 .
.
В случае балки имеем:
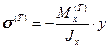 .
.
По закону Гука:
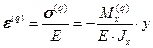 .
.
Отсюда:

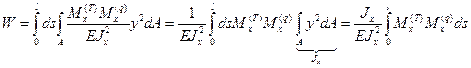
Запишем закон сохранения энергии:

Отсюда вытекает формула Мора:

 (16.2)
(16.2)
Здесь 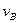 - искомый прогиб в точке B (от рабочих нагрузок);
- искомый прогиб в точке B (от рабочих нагрузок);
 =1 – единичная сила, приложенная в интересующем нас направлении искомого прогиба
=1 – единичная сила, приложенная в интересующем нас направлении искомого прогиба 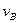 в интересующей нас точке В.
в интересующей нас точке В.
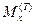 - изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.
- изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.
 - изгибающий момент от рабочих нагрузок.
- изгибающий момент от рабочих нагрузок.
Физический смысл формулы Мора заключается в следующем: работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.
Примечания.
1. Работой касательных напряжений 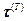 обычно пренебрегают ввиду ее малости по сравнению с W.
обычно пренебрегают ввиду ее малости по сравнению с W.
 2. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид
2. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m в интересующей нас точке. Формула Мора примет вид
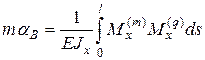 .
.
Дата добавления: 2015-11-28; просмотров: 1356;
