Вычисление прогибов на основе решения дифференциального уравнения изогнутой оси балки
Прогибы можно находить и другими способами, например, на основе решения дифференциального уравнения изогнутой оси балки. Для вывода этого уравнения, рассмотрим элемент балки (рис.16.6).
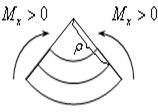
Рис. 16.6
Ясно, что чем больше  , тем больше кривизна
, тем больше кривизна 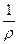 изогнутой оси балки.
изогнутой оси балки.
Эту фразу можно записать в виде:
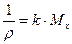 . (16.5)
. (16.5)
Выразим кривизну через прогиб. Согласно формулам математического анализа:

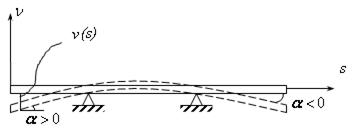
Рис.16.7
По геометрическому смыслу производная это тангенс угла наклона кривой (рис16.7):
 .
.
Ввиду малости прогибов угол 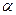 также мал, поэтому
также мал, поэтому
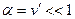 .
.
Тогда: 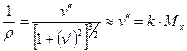 (16.6)
(16.6)
Очевидно, что k зависит от геометрии сечения и материала балки. Найдем эту зависимость.
Рассмотрим малый элемент балки длины 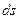 (рис. 16.3, 16.4). После изгиба он превратится в изогнутый элемент (рис.16.8). Длина волокна BC, которое проходит через центр тяжести сечения, не изменяется и будет равна
(рис. 16.3, 16.4). После изгиба он превратится в изогнутый элемент (рис.16.8). Длина волокна BC, которое проходит через центр тяжести сечения, не изменяется и будет равна 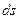 . А нижнее волокно DH удлиняется на
. А нижнее волокно DH удлиняется на  .
.
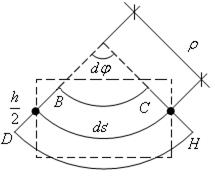
Рис.16.8
Вычисляем  , учитывая, что
, учитывая, что 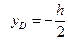 . Согласно определению
. Согласно определению
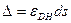 .
.
Используя закон Гука и формулу Навье получаем
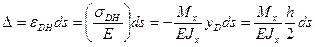 . (16.7)
. (16.7)
Вычислим  теперь по другому - через угол
теперь по другому - через угол  (рис.16.8). Из геометрии известна формула для вычисления длины дуги:
(рис.16.8). Из геометрии известна формула для вычисления длины дуги:
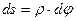 .
.
Тогда
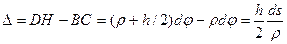 . (16.8)
. (16.8)
Приравниваем (16.7) и (16.8):
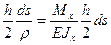 .
.
Отсюда получаем:
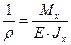 .
.
Учитываем, что согласно (16.6):
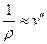
Окончательно получаем:

| (16.9) |
Это и есть уравнение изогнутой оси балки.
Дата добавления: 2015-11-28; просмотров: 969;
