Решение дифференциального уравнения изогнутой оси балки

Если балка имеет постоянную толщину, то есть 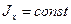, то решение легко записывается в общем виде:

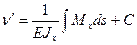(16.10)

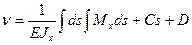(16.11)

Хотя решение получено в общем виде, однако основная трудность заключается в определении М_х иконстант C и D, поскольку на разных участках балки разные, а значит C и D также разные (в частности, если балка имеет три участка, то нужно определить 6 констант C и D).

Однако существует способ интегрирования, который сводит все неизвестные только к двум константам (разработан Клебшом)

Правила Клебша

Правила Клебша сводятся к следующему.

1) выражаем через внешние силы, которые лежат только слева (или только справа) от сечения.

2) Если погонная сила q не доходит до правого конца, то ее доводим до этого правого конца и уравновешиваем ее снизу (рис.16.9)

Рис.16.9

3) Если имеется сосредоточенный момент m_о, то его вклад записываем в виде 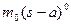, где а - расстояние до момента m_о.

4) Интегрируем, не раскрывая скобок.

При выполнении этих условий все константы С на разных участках будут одинаковы. Аналогично будут одинаковы все константы D.

Справедливость правил Клебша доказывается непосредственной проверкой, то есть подстановкой решения в условия стыковки решения на границе участков. Рассмотрим, например, случай, приведенный на рис.16.12.

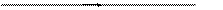
рис16.12

По правилам Клебша момент на участках (1), (2) запишем в виде:

(1):

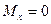
(2):

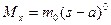
Дифференциальные уравнения на участках:

(1)

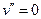
(2)

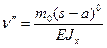
Решение этих уравнений на участках (1), (2) имеет вид:

Участок (1): .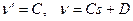

Участок (2): .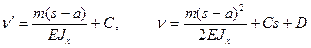

Отсюда видно, что при S = a получим равенство углов наклона и прогибов, вычисленных по разным формулам при любых С и D, т.е. условия гладкости изогнутой оси выполняются. Аналогично проверяются условия гладкости на границе участка, на которой заканчивается погонная сила q.

16.2.3 Условия для определения С и D

1) Первый случай .Рассмотрим балку, лежащую на двух опорах (см. рис.16.10).

Рис. 16.10

Рис. 16.11

Из схемы видно, что

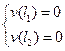(16.13)

Таким образом, получаем систему уравнений для С и D.

2) Второй случай. Пусть балка заделана на расстоянии 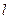(консольная балка, см. рис.16.10).

В заделке не может появиться наклона оси, поэтому там не только нет прогиба, но и .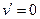

Таким образом, из схемы следует, что:

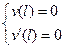(16.14)

Опять получили два уравнения для С и D.

 

Пример вычисления прогиба

Пусть необходимо вычислить прогиб в центре балки длины l, загруженной погонной силой q. Решим эту задачу двумя способами.

Ввиду симметричности схемы можно сразу найти реактивные силы – они будут равны ql/2. Тогда изгибающий момент в сечении на расстоянии z от левой опоры будет равен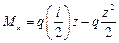

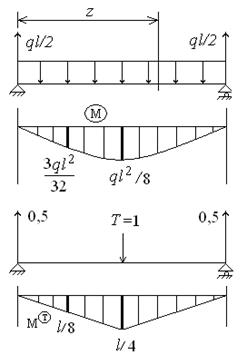
Первый способ. Использование дифференциального уравнения изогнутой оси балки. 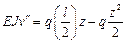Интегрируем 2 раза: 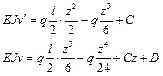Константы интегрирования находим из условий закрепления: 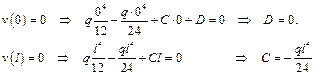Находим прогиб в центре балки (при z = l/2):

 

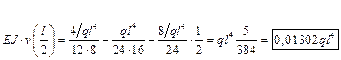
Второй способ. Использование интеграла Мора

Прогиб в центре балки находим по формуле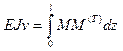

Нарисуем эпюру изгибающих моментов М^(T) от единичной силы Т=1 (см. рис.2)

Рассмотрим различные приближенные методы интегрирования.

1. Метод трапеций по 2-м участкам.

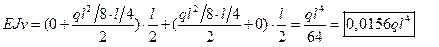
Метод дал ошибку в 17%

2. Метод трапеций по 4-м участкам.

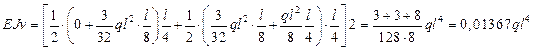
Метод дал ошибку в 5%

3. Метод Симпсона по 2-м участкам.

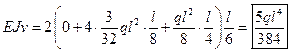
Таким образом, метод Симпсона в этом примере дает точное решение.