Потеря устойчивости
Рассмотрим сжатый стержень.
 |  |
рис.17.1 рис.17.2
Пусть сила Р приложена в центре тяжести сечения стержня. На первый взгляд у силы Р нет плеча, значит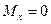 
, значит, для изгиба нет причин.
Это справедливо при малых Р. Однако при некотором значении Р происходит резкая смена прямолинейной формы в криволинейную при малейшем поперечном воздействии (см.рис.17.2)
Это явление называется потерей устойчивости.
Сила Р, при которой это происходит, называется критической, а соответствующее ей напряжение называют критическим напряжением:
.
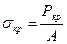Опыт показывает, что для потери устойчивости стержня требуется меньшая сила, чем для разрушения , например, кубика из того же материала сжатием. Таким образом:
, 
.
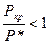здесь Р* - разрушающая сила.
Уменьшая критическое напряжение σкр на коэффициент запаса kуст получают допустимое напряжение [σ]уст , больше которого не должно быть рабочее напряжение:
|σ| ≤[σ]уст.
Для удобства расчетов часто пользуются таблицами, в которых приводится коэффициент φ, показывающий, насколько [σ]уст меньше основного допустимого напряжения [σ]:
φ=[σ]уст / [σ].
Если на растяжение и сжатие разрушающие напряжения различны, то под φ понимают величину:
φ=[σ]уст / [σ]сж.
Формула Эйлера
Впервые формулу для вычисления 
вывел Л. Эйлер.
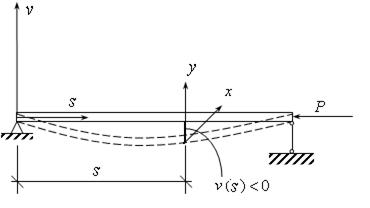
рис.17.3
Рассмотрим балку, потерявшую устойчивость, т.е.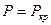 
(см. рис.17.3)
Изгиб здесь имеет место под действием момента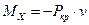 
, где v – прогиб. Для отыскания 
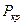используем уравнение изогнутой оси балки:
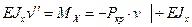
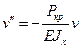(17.1)
Получили дифференциальное уравнение для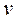 
.
Обозначим
.
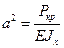Тогда
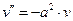(17.2)
Решение этого уравнения можно записать в виде:
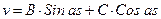(17.3)
т.к. легко проверить, что слева в (17.2) получиться то же самое, что и справа.
Константы В и С отыскиваем из условий закрепления:
(1): 
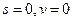на левом краю
(2): 
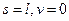на правом краю
Это дает:
(1): 
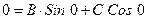на левом краю
(2): 
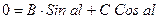на правом краю
Отсюда
(1): 
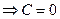
(2): 
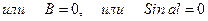
При 
, значит прогиба нет, т.е. нет потери устойчивости. Поскольку это противоречит исходному предположению, то рассмотрим уравнение
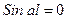
Оно имеет следующие решения:
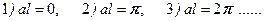, (17.4)
где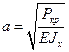 
Рассмотрим решения (17.4).
1) 
- это решение не подходит, т.к. стержень не изогнется без нагрузки.
2) 
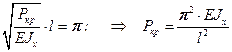
3) 
,
Второе решение дает: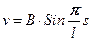 
(см. рис. 17.4)
Третье решение дает: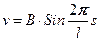 
(см. рис. 17.5)
 |  |
Рис. 17.4 Рис. 17.5
Ясно, что при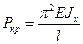 
уже произойдет изгиб, и дальнейшее повышение нагрузки невозможно, т.е. до величины 
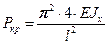нагрузка Р увеличиться не может. Аналогично и для других решений (17.4). Таким образом, получим что:
(17.5)
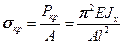(17.6)
Мы рассмотрели изгиб в вертикальной плоскости, аналогично можно рассмотреть изгиб в горизонтальной плоскости, тогда получим:
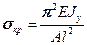(17.7)
Очевидно, что изгиб произойдет в той плоскости, которая требует меньшее значение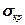 
. Видно, что 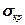в (17.6) и (17.7) отличаются только моментом инерции. Таким образом, нужно взять тот случай, в котором момент инерции меньше:
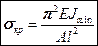(17.8)
Известно, что момент инерции достигает наименьшего значения относительно одной из главных центральных осей. Следовательно, для вычисления 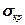необходимо найти главные центральные оси и главные моменты, а затем выбрать из них наименьшее.
Важные примечания.
1) Здесь предполагалось, что в обеих плоскостях опоры - шарнирные.
2) При выводе формулы предполагалось, что стержень упругий и соблюдается закон Гука, поскольку уравнение изогнутой оси балки получено при условии, что стержень линейно упругий. Таким образом, формула верна только тогда, когда справедлив закон Гука.
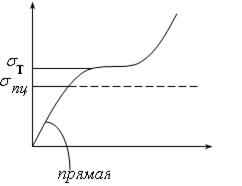
Рис. 17.6
Таким образом, формула Эйлера справедлива только тогда, когда:
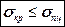(17.9)
3).. Вывод формулы Эйлера можно провести и из других соображений, а именно из закона сохранения энергии, полагая что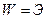 
, где
, 
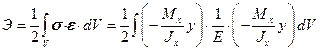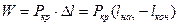
Дата добавления: 2015-11-28; просмотров: 682;