Предельная гибкость. Длинный стержень.

Рассмотрим условие применимости формулы Эйлера (17.9):

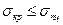
Подставим сюда (17.14):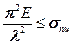

Отсюда: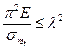

Или: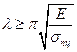

Обозначим правую часть через:

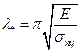
Таким образом, формула Эйлера применима, если:

То есть, если условная длина достаточно большая, то формула Эйлера применима. Поэтому такие стержни называют длинными.

Формула Ясинского.

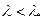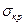Он изучил более 2000 экспериментов и показал, что если , то можно вычислять по формуле:

Это и есть формула Ясинского.

Здесь a и b константы материала. Например, для стали:

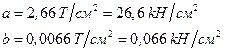
Кроме того, для стали предел текучести

Из формулы Ясинского видно, что если 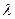очень мал, то

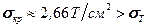
Это означает, что для изгиба стержня-образца требуется больше усилий, чем для того, чтобы сплющить этот образец. Поэтому формула Ясинского справедлива только тогда, когда:

Это условие применимости формулы Ясинского.

Отсюда 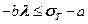, или

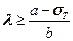
Если ,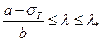

то этот стержень называют стержнем средней длины.

Если же:

,

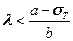то стержень называют коротким:

Продольный изгиб

Снова рассмотрим изгиб балки под действием продольной центральной силы Р, но предварительно изогнутой приложенными по концам сосредоточенными моментами m (см. рис. 17.12). Этот момент может быть вызван внецентренным нагружением продольной силой Р, если он имеет эксцентриситет е, то m=Ре.

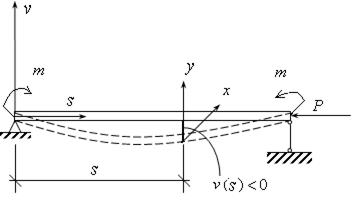
Рис. 17.12

Уравнение изогнутой оси примет вид

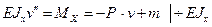
Деля на 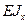и принимая уже использованное выше обозначение 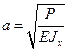, решение этого уравнения запишем в виде

Как и при выводе формулы Эйлера, константы В и С отыскиваем из условий закрепления:

(1): 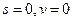на левом краю

(2): 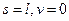на правом краю

Это дает:

(1): 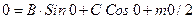на левом краю

(2): 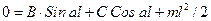на правом краю

Отсюда

(1):

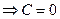
(2):

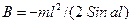
При Р=Р_кр ,то есть при 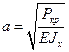, имеем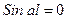

Тогда из выражения для В вытекает, что

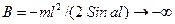
Следовательно, при Р→Р_кр получаем неограниченно большие прогибы:

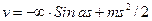
Таким образом, при внецентренном нагружении (или при наличии предварительного изгиба) балка может выдержать продольную сжимающую силу, которая не может быть больше Р_кр

Кручение валов