Другие условия закрепления.

Рис. 17.7

Будем пользоваться геометрической аналогией. Эта задача аналогична приведенной ниже:

Рис. 17.8

Правая её половина точно такая же, как рассматриваемая балка, следовательно:

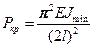
Рассмотрим теперь случай защемления с двух концов:

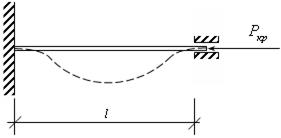
Рис. 17.9

Здесь только половина балки, а именно её серединная часть изгибается как шарнирная:

Рис. 17.10

Таким образом:

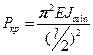
Введем параметр n – число волн, которые образуются при продольном изгибе балки, тогда получим:

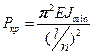
Пользуясь этой аналогией, получим еще одну (приближенную) формулу для случая, изображенного на рис. 17.11:

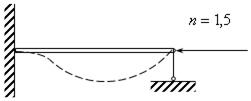
Рис. 17.11

В расчетной практике вместо n используют - коэффициент приведенной длины :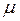

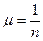
Запишем формулу Эйлера с помощью нового обозначения:

(17.10)

Кроме того, в теории устойчивости вводят параметр:

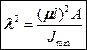(17.11)

Здесь 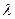- безразмерная величина, являющаяся относительной длиной, называется гибкостью.

Для корня 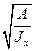вводят специальное обозначение:

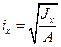(17.12)

Аналогично,

(17.13)

Величины 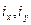- называются радиусами инерции сечения.

В новых обозначениях получим:

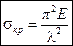(17.14)

Это наиболее употребительный вид формулы Эйлера.