Соотношения неопределенностей

Опыты по дифракции электронов и других микрочастиц показали, что микрочастица не является материальной точкой, а представляет собой сложный материальный объект, обладающий волновыми свойствами.

В связи с этим встал вопрос о границах применимости классической физики в микромире. Критерием применимости классической физики в микромире являются соотношения неопределенностей.

В классической механике состояние частицы определяется заданием координат x,y,z и импульса 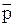(p_x, p_y, p_z) в каждый момент времени. Принимается, что эти динамические переменные могут быть измерены с любой нужной степенью точности. Однако волновые свойства микрочастиц приводят к тому, что микрочастица не может иметь одновременно точных значений координаты xи составляющей импульса р_x ( y и р_y, z и р_z ).

Математически:

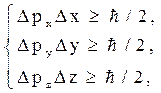(5.9)

где ħ = h / 2p.

Соотношения (5.9) называются соотношениями неопределенностей Гейзенберга. Аналогичные соотношения имеют место для ряда других пар величин (энергия и время, компоненты момента импульса и т.д.). Такие величины называются каноническими сопряженными переменными.

Принцип неопределенностей Гейзенберга формулируется следующим образом: произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка ħ.

В квантовой механике доказывается, что эти соотношения носят самый общий характер и выполняются при движении любых тел.

Таким образом, волновая природа микрочастиц приводит к тому, что микрочастица не может иметь одновременно определенные значения координаты x и импульса р_х (y и p_y, z и p_z). Из (5.9) следует, что чем с большей точностью определяется координата частицы, тем с меньшей точностью можно определить ее импульс, и наоборот.

Это значит, что состояние микрочастицы можно охарактеризовать с помощью величин, присущих классической частице, лишь с некоторым приближением, которое устанавливается соотношением неопределенностей.

Соотношение неопределенностей, аналогичное (5.9), существует для времени и энергии:

(5.10)

Выражение (5.10) означает, что определение энергии с точностью до (Е±DE) должно занять интервал времени Dt, не меньший чем:

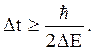
Соотношение (5.10) приводит к важным выводам относительно возбужденных состояний ядер, атомов и молекул. Если Dt – время жизни возбужденного состояния (Dt ~10^–8 с), то неопределенность энергии этого состояния

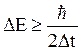~10 ^–26 Дж.

Неопределенность энергии DЕ называется естественной шириной энергетического уровня.

Следовательно, при переходе атома из возбужденного состояния в невозбужденное или в менее возбужденное излучается фотон, энергия которого определяется с точностью до DЕ, а частота имеет неопределенность:

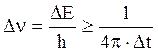или 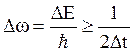~ 10⁸ рад/с.

Неопределенность Dn (Dw) называется естественной шириной спектральной линии. Эта неопределенность оказывается настолько большой, что атомами излучаются не отдельные спектральные линии, а целые спектральные участки шириной Dn. По ширине спектральной линии можно определить время жизни атома в возбужденном состоянии.

5.4. Волновая функция и её свойства

Интенсивность волн де Бройля в данной точке пространства связана с числом частиц, попавших в эту точку, о чем свидетельствуют опыты по дифракции микрочастиц. Поэтому волновые свойства микрочастиц требуют статистического (вероятностного) подхода к их описанию.

Для описания поведения квантовых систем вводится волновая функция (или пси-функция) Y(x,y,z,t). Она определяется таким образом, чтобы вероятность dw того, что частица находится в объеме dV, была равна:

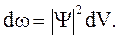(5.11)

Физический смысл имеет не сама функция Y, а квадрат её модуля 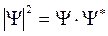, которым задается интенсивность волн де Бройля (здесь Y^* - функция, комплексно сопряженная с Y). Величина 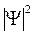имеет смысл плотности вероятности r_w:

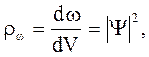(5.12)

а сама волновая функция имеет смысл амплитуды вероятности.

Условие нормировки вероятностей получается из того, что вероятность существования частицы где-либо в пространстве равна единице (интеграл вычисляется по всему бесконечному пространству):

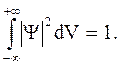(5.13)

Волновая функция, характеризующая вероятность обнаружения частицы в элементе объема, должна быть:

1) конечной (вероятность не может быть больше единицы);

2) однозначной (вероятность не может быть неоднозначной величиной);

3) непрерывной (вероятность не может изменяться скачкообразно).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Y₁, Y₂, …, Y_n, …, то она также может находиться в состоянии, описываемом линейной комбинацией этих функций:

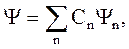(5.14)

где C_n (n = 1, 2, ...) – комплексные числа.