Уравнение Шредингера для стационарных состояний

Важным частным случаем общего уравнения Шредингераявляется уравнение Шредингера для стационарных состояний, в котором исключена зависимость Y от времени, и поэтому значения энергии этих состояний являются фиксированными (не изменяются со временем).

В этом случае силовое поле, в котором движется частица, стационарно, т.е. функция 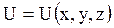не зависит явно от времени и имеет смысл потенциальной энергии. Решение уравнения может быть представлено в виде произведения двух функций – функции только координат и функции только времени

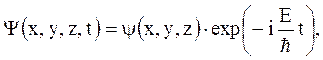(5.16)

где E – полная энергия частицы.

Уравнение Шредингера

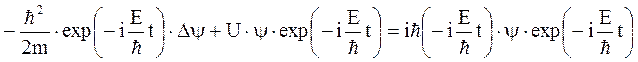
после упрощений приобретает вид:

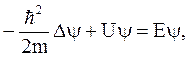
или

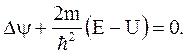(5.17)

Выражение (5.17) – уравнение Шредингера для стационарных состояний.

Физический смысл имеют только регулярные волновые функции – конечные, однозначные и непрерывные – вместе со своими первыми производными. Данные условия выполняются только при определенном наборе E. Эти значения энергии называются собственными. Решения, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения E могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном (сплошном) спектре, во втором – о дискретном спектре.