Корпускулярно-волновой дуализм свойств вещества

Основными характеристиками света как волнового процесса являются частота n и длина волны l. Корпускулярные свойства света характеризуются фотонами. Каждый фотон обладает энергией

e_ф = hn, (5.1)

массой

(5.2)

и импульсом

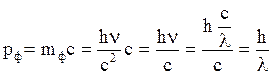. (5.3)

Формула (5.3) устанавливает связь волновых и корпускулярных свойств света.

В связи с этим возникло предположение о том, что двойственная природа присуща не только свету, но и частицам материи, в частности электрону. В 1924 году Луи де Бройль высказал следующую гипотезу: с электроном связан волновой процесс, длина волны которого равна

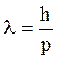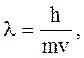или (5.4)

где h = 6,63 × 10^–34 Дж×с — постоянная Планка, m – масса электрона, v – скорость электрона.

Расчеты показали, что длина волны, связанной с движущимся электроном, имеет тот же порядок, что и длина волны рентгеновских лучей (10^–10 ¸ 10^–13 м).

Из формулы де Бройля (5.4) видно, что волновые свойства частиц существенны только в тех случаях, в которых величиной постоянной Планка h пренебречь нельзя. Если в условиях данной задачи можно считать, что h ® 0, то и l®0 и волновыми свойствами частиц можно пренебречь.

5.2. Опытное обоснование корпускулярно – волнового дуализма

Гипотеза де Бройля получила экспериментальное подтверждение в опытах К. Дэвиссона и Л. Джермера (1927 г.), П.С. Тартаковского (1927 г.), Л.М. Бибермана, Н.Г. Сушкина и В.А. Фабриканта (1949 г.) и др.

В опытах Дэвиссона и Джермера (рис.5.1) электроны из электронной пушки узким пучком направлялись на кристалл никеля, структура которого хорошо известна.

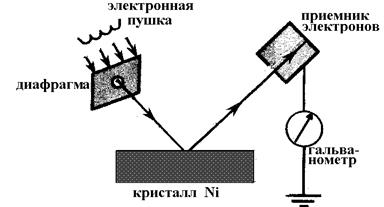
Рис.5.1. Схема опыта Девиссона и Джермера

Отраженные от поверхности кристалла электроны попадали в приемник, соединенный с гальванометром. Приемник перемещался по дуге и улавливал электроны, отраженные под разными углами. Чем больше электронов попадало в приемник, тем больший ток регистрировался гальванометром.

Оказалось, что при заданном угле падения электронного пучка и изменении разности потенциалов U, ускоряющей электроны, ток I менялся не монотонно, а имел ряд максимумов (рис.5.2).

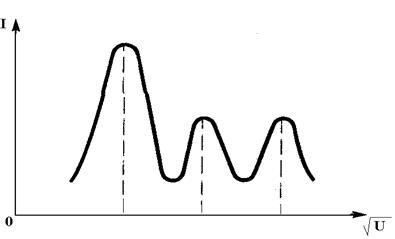
Рис.5.2. Зависимость силы тока от ускоряющей разности потенциалов в опытах Дэвиссона и Джермера

Полученный график говорит о том, что отражение электронов происходит не при любых, а при строго определенных значениях U, т.е. при строго определенных скоростях v электронов. Эту зависимость удалось объяснить только на основе представлений об электронных волнах.

Для этого выразим скорость электрона через ускоряющее напряжение:

,

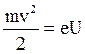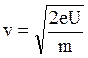(5.5)

и найдем дебройлевскую длину волны электрона:

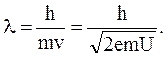(5.6)

Для отраженных от кристалла электронных волн, так же как и для рентгеновских лучей, должно выполняться условие Вульфа-Брэггов:

2d sinq = kl, k = 1,2,3,..., (5.7)

где d – постоянная кристаллической решетки, q – угол между падающим лучом и поверхностью кристалла.

Подставив (5.6) в (5.7), найдем те значения ускоряющего напряжения, которые соответствуют максимумам отражения, а следовательно, и максимальному току через гальванометр:

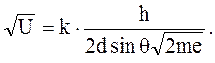(5.8)

Рассчитанные по данной формуле значения U при q=const прекрасно согласуются с результатами опытов Дэвиссона и Джермера.

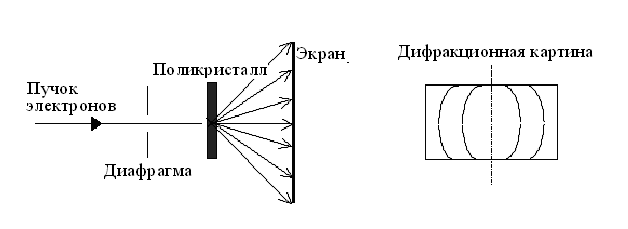
В опытах П.С. Тартаковского кристалл заменялся тонкой пленкой поликристаллической структуры (рис.5.3).

Рис.5.3. Схема опытов П.С. Тартаковского

Рассеянные пленкой электроны давали на экране дифракционные круги. Аналогичная картина наблюдалась при рассеянии рентгеновских лучей на поликристаллах. По диаметрам дифракционных кругов можно определить дебройлевскую длину волны lэлектронов. Если l известна, то дифракционная картина позволяет судить о структуре кристалла. Этот метод исследования структуры носит название электронографии.

Л.М. Биберманом, Н.Г. Сушкиным и В.А. Фабрикантом были осуществлены опыты по дифракции одиночных, поочередно летящих электронов. Отдельные электроны попадали в различные точки экрана, на первый взгляд, разбросанные беспорядочно. Однако при рассеянии большого числа электронов обнаружилось, что точки попадания электронов на экран распределены так, что образуют максимумы и минимумы, т.е. при длительной экспозиции была получена такая же дифракционная картина, какую дает пучок электронов. Это свидетельствует о том, что волновыми свойствами обладает каждый отдельно взятый электрон.

Дифракционные явления наблюдались в опытах не только с электронами, но и с протонами, нейтронами, атомными и молекулярными пучками.