Напряженность магнитного поля. Связь между индукцией и напряженностью магнитного поля
Пусть некоторый контур с током создает магнитное поле. Если все пространство заполнено изотропным веществом с магнитной проницаемостью m1[1], то в выбранной точке значение магнитной индукции будет 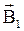 . При заполнении всего пространства другим веществом с магнитной проницаемостью m2 магнитная индукция в той же точке примет значение
. При заполнении всего пространства другим веществом с магнитной проницаемостью m2 магнитная индукция в той же точке примет значение 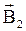 и т.д. Отношение же B/mm0 (где m0 – абсолютная магнитная проницаемость вакуума: m0 = 4p × 10-7 Гн/м) будет во всех случаях одинаково. Величину, равную отношению
и т.д. Отношение же B/mm0 (где m0 – абсолютная магнитная проницаемость вакуума: m0 = 4p × 10-7 Гн/м) будет во всех случаях одинаково. Величину, равную отношению
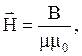 (4.4)
(4.4)
называют напряженностью магнитного поля.
Напряженность магнитного поля не зависит от свойств среды, а зависит от силы тока, протекающего по контуру, формы контура и расположения его относительно выбранной точки. Направления векторов 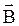 и
и 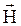 в изотропной среде совпадают.
в изотропной среде совпадают.
4.2. Закон Био – Савара – Лапласа
Ученые Био и Савар экспериментально установили, что величина 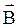 зависит от величины тока, размеров и формы проводников, расстояния от проводников до точки, в которой находят величину
зависит от величины тока, размеров и формы проводников, расстояния от проводников до точки, в которой находят величину 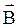 . Лаплас обобщил результаты экспериметов Био и Савара и установил, что поле любого тока может быть вычислено как векторная сумма полей, созданных элементарными участками тока.
. Лаплас обобщил результаты экспериметов Био и Савара и установил, что поле любого тока может быть вычислено как векторная сумма полей, созданных элементарными участками тока.
Итак, имеем проводник, по которому течет ток I (рис.4.3). Выберем на нем прямолинейный элемент тока 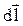 .
.
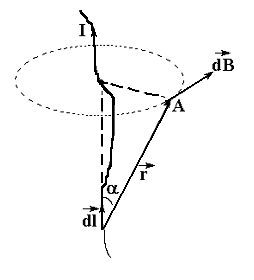 Рис.4.3
Рис.4.3
| Вектор 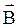 зависит от многих параметров: зависит от многих параметров:
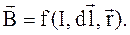 (4.5)
Магнитная индукция поля, созданного элементарным участком проводника, как следует из эксперимента, равна: (4.5)
Магнитная индукция поля, созданного элементарным участком проводника, как следует из эксперимента, равна:
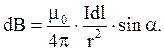 (4.6)
В векторной форме: (4.6)
В векторной форме:
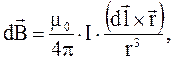 (4.7) (4.7)
|
где dB – значение магнитной индукции, создаваемой элементом тока dlна расстоянии rот проводника; m0 – абсолютная магнитная проницаемость вакуума;
I– сила тока в проводнике; a - угол между направлением элемента  и радиусом-вектором
и радиусом-вектором 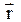 .
.
Таким образом, 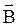 прямо пропорционален векторному произведению
прямо пропорционален векторному произведению  .
.
4.2.1. Применение закона Био-Савара–Лапласа для вычисления значения вектора 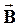
1. Поле движущегося электрического заряда
Запишем закон Био-Савара-Лапласа в векторной форме:
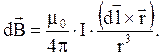
Заменим произведение Idl на s∙jdl, а j, как известно, равно j=n∙e∙u, где s – площадь сечения, j – плотность тока, n – число зарядов в единице объема, е – величина электрического заряда, u – средняя скорость упорядоченного движения зарядов.
Указанные выше соотношения справедливы, т.к. векторы 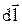 и
и 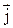 имеют одинаковое направление. Векторы
имеют одинаковое направление. Векторы 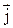 и
и 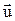 направлены одинаково, если заряд положительный, и противоположно, если заряд отрицательный. Подставим выражения
направлены одинаково, если заряд положительный, и противоположно, если заряд отрицательный. Подставим выражения 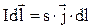 и
и 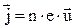 в формулу для
в формулу для 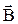 :
:
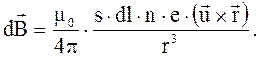
Произведение sdl=dV - объем рассматриваемого проводника dl, dV∙n - число зарядов в данном элементе проводника.
Поле 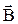 , созданное одним зарядом, получим путем деления выражения для
, созданное одним зарядом, получим путем деления выражения для 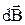 на dV∙n.
на dV∙n.
Тогда
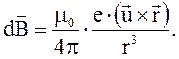 (4.8)
(4.8)
2. Поле, созданное бесконечно длинным проводником (прямым током)
Найдем величину 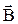 в произвольной точке А (рис.4.4). Проведем силовую линию через точку А.
в произвольной точке А (рис.4.4). Проведем силовую линию через точку А.
Рис.4.4
Из рис.4.4 видно, что в данном случае поле, созданное каждым участком проводника  , будет перпендикулярно плоскости чертежа и направлено за чертеж. Значит, результирующее поле можно найти суммированием модулей векторов
, будет перпендикулярно плоскости чертежа и направлено за чертеж. Значит, результирующее поле можно найти суммированием модулей векторов  . По закону Био-Савара-Лапласа модуль вектора
. По закону Био-Савара-Лапласа модуль вектора 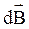 равен:
равен:
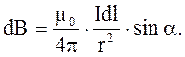
Преобразуем выражение для dB, используя соотношения, полученные нами из рис.4.4:
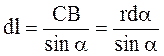 ;
; 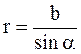 ;
;
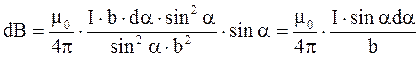 ;
;
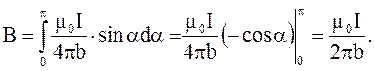 (4.9)
(4.9)
Угол α изменяется для бесконечно длинного проводника от 0 до p, в чем можно убедиться, взяв участок dl на большом удалении справа и слева от точки А.
Поле тока конечной длины
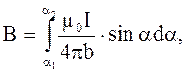
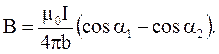 (4.10)
(4.10)
3. Магнитное поле кругового тока
а) Найдем циркуляцию 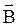 магнитного поля в центре витка радиусом R, по которому протекает ток I (рис.4.5).
магнитного поля в центре витка радиусом R, по которому протекает ток I (рис.4.5).
Разобьем весь круговой виток на элементы тока 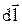 .
.
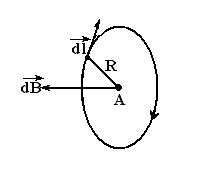 Рис.4.5
Рис.4.5
| Тогда по закону Био-Савара-Лапласа магнитная индукция 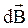 , создаваемая в точке О элементом , создаваемая в точке О элементом 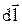 , равна: , равна:
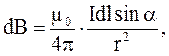 где r = R; a = p/2 (для любого элемента
где r = R; a = p/2 (для любого элемента 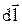 ); sina = 1.
Получаем: ); sina = 1.
Получаем:
|
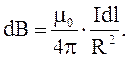
Все векторы 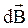 , создаваемые в точке Округового витка, направлены перпендикулярно к плоскости витка за чертеж.
, создаваемые в точке Округового витка, направлены перпендикулярно к плоскости витка за чертеж.
Тогда

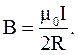 (4.11)
(4.11)
б) Если т. А лежит на оси кругового тока, вектор 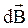 должен быть перпендикулярен наклонной плоскости, образованной векторами
должен быть перпендикулярен наклонной плоскости, образованной векторами 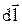 и
и 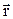 (рис.4.6).
(рис.4.6).
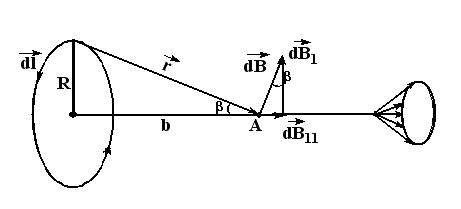
Рис.4.6
Отсюда следует, что 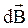 направлен под углом к оси. Как следует из геометрии, угол между вектором
направлен под углом к оси. Как следует из геометрии, угол между вектором 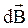 и вертикалью равен β. Из соображений симметрии легко представить, что разные участки кругового тока создадут веер векторов
и вертикалью равен β. Из соображений симметрии легко представить, что разные участки кругового тока создадут веер векторов 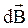 . Составляющие вектора
. Составляющие вектора 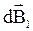 друг друга скомпенсируют, т.к. для симметричных относительно оси и одинаковых участков
друг друга скомпенсируют, т.к. для симметричных относительно оси и одинаковых участков 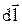 они направлены в противоположные стороны и равны. Составляющие
они направлены в противоположные стороны и равны. Составляющие  от всех участков
от всех участков 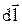 направлены в одну сторону по оси – их сумма и есть результирующий вектор
направлены в одну сторону по оси – их сумма и есть результирующий вектор 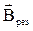 :
:
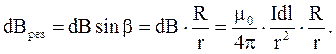
Угол между 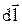 и
и 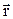 равен 90°, синус этого угла равен единице. Тогда
равен 90°, синус этого угла равен единице. Тогда
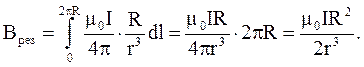
Учитывая, что R2 + b2 = r2 , запишем:
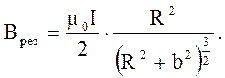 (4.12)
(4.12)
Дата добавления: 2016-01-07; просмотров: 4608;
