Закон Джоуля-Ленца в дифференциальной форме

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через сечение проводника проходит заряд q:

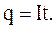
При этом силы кулоновского поля и поля сторонних сил совершают работу

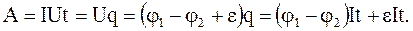
В случае, когда проводник неподвижен и никаких химических превращений в нем не совершается, эта работа идет на увеличение внутренней энергии проводника, в результате чего проводник нагревается. При протекании тока в проводнике выделяется тепло Q:

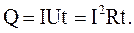(3.60)

(3.60) – закон Джоуля-Ленца.

Если цепь неоднородная, то в различных ее участках выделяется разное количество тепла.

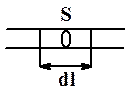Рис.3.19

Выделим малый участок проводника dl сечением S (рис.3.19). Количество тепла, выделяющегося на участке dl: 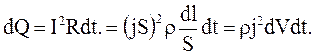(3.61) Разделим обе части уравнения (3.61) на dV и dt:

(3.62)

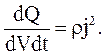(3.62) – количество тепла, выделяющегося в единице объема за единицу времени, или плотность тепловой мощности w:

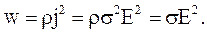(3.63)

(3.63) – закон Джоуля –Ленца в дифференциальной форме.

Плотность тепловой мощности прямо пропорциональна квадрату напряженности поля и проводимости проводника.

Электромагнетизм