Закон Ома в интегральной и дифференциальной форме
 Рис.3.16
Рис.3.16
| Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а j1 и j2 – потенциалы на концах проводника (рис.3.16). В случае однородного проводника величину j1 - j2 = U можно назвать падением напряжения на участке проводника. |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:
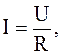 (3.47)
(3.47)
где R – электрическое сопротивление проводника.
(3.47) – закон Ома в интегральной форме.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника
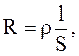 (3.48)
(3.48)
где r - удельное сопротивление проводника.
Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2. Размерность удельного сопротивления в СИ: [r] = Ом×м.
Величина, обратная сопротивлению, называется проводимостью.
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
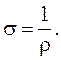 (3.49)
(3.49)
Единица, обратная Ом, называется Сименсом [См].
Учитывая (3.46) - (3.49), а также 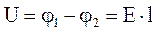 , получим:
, получим:
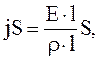
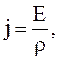
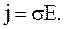 (3.50)
(3.50)
(3.50) – закон Ома в дифференциальной форме.
Дата добавления: 2016-01-07; просмотров: 982;
