Базовые соотношения для линейных электрических цепей

Закон Ома. Связь между током и напряжением на линейном резисторе описывается законом Ома:

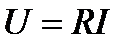, (2.12.)

где R – сопротивление резистора.

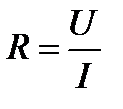
Рис.2.13. Иллюстрация использования закона Ома

Первый закон Кирхгофа (правило узлов). При расчете многих схем используется правило узлов, согласно которому сумма всех токов, протекающих через узел, равна нулю. При этом ток, направленный к узлу, считается положительным, а ток, направленный от узла – отрицательным. Использование правила узлов демонстрируется на схеме 2.14, где

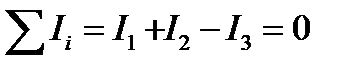. (2.13)

Рис.2.14. Пример использования правила узлов

Второй закон Кирхгофа. Согласно этому закону, сумма всех напряжений замкнутой цепи равна нулю. При этом положительными считаются напряжения, направления которых совпадают с выбранным направлением тока. Напряжения противоположного направления считаются отрицательными. Следовательно, в схеме, изображенной на рис.2.15:

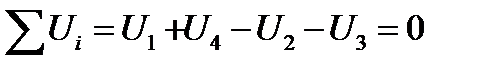. (2.14)

Рис.2.15. Пример использования второго закона Кирхгофа

Полное и реактивное сопротивление. Схемы с конденсаторами и индуктивностями сложнее, чем рассмотренные ранее резистивные схемы – их работа зависит от частоты входного сигнала: «делитель напряжения» с конденсатором или индуктивностью будет обладать частотно-зависимым коэффициентом деления. Кроме того, схемы, в состав которых входят эти компоненты (их, кстати, относят к классу пассивных), искажают такие входные сигналы, как, например, прямоугольные колебания.

Однако и конденсаторы, и индуктивности являются линейными элементами. Это означает, что амплитуда выходного сигнала, независимо от его формы, строго пропорциональна амплитуде входного сигнала. Линейностью обусловлены многие закономерности поведения схем и важнейшая состоит в следующем: если ни вход линейной схемы подан синусоидальный сигнал с частотой f, то на выходе будет получен также синусоидальный сигнал с такой же частотой, но, возможно, с другой амплитудой и фазой.

Учитывая это свойство при анализе схем, содержащих резисторы, конденсаторы и индуктивности, всегда можно ответить на вопрос: как зависит выходное напряжение (его амплитуда и фаза) от входного напряжения в виде синусоидального сигнала определенной частоты. Этот вопрос важен и тогда, когда схема предназначена для другого режима работы. График результирующей амплитудно-частотной характеристики, отражающей отношение выходного сигнала к входному для каждого значения частоты синусоиды, полезен при анализе работы схемы со многими видами сигналов.

Можно обобщить закон Ома, заменив понятие «сопротивление» понятием «полное сопротивление», или «импеданс». Тогда он будет справедлив для любой схемы, в состав которой входят линейные пассивные элементы (резисторы, конденсаторы, индуктивности). Итак, понятия «импеданс» и «реактивное сопротивление» делают закон Ома справедливым для схем, содержащих конденсаторы и индуктивности. Импеданс – это обобщенное или полное сопротивление, индуктивности и конденсаторы обладают реактивным сопротивлением, резисторы обладают сопротивлением. Иными словами, импеданс = сопротивление + реактивное сопротивление.

Однако можно встретить, например, такое выражение: «импеданс конденсатора на данной частоте составляет…». Дело в том, что в импеданс входит реактивное сопротивление, и поэтому не обязательно говорить «реактивное сопротивление конденсатора», можно сказать и «импеданс конденсатора». На самом деле слове «импеданс» часто употребляют и тогда, когда известно, что речь идет о сопротивлении, например, говорят «импеданс источника» или «выходной импеданс», имея в виду эквивалентное сопротивление некоторого источника. То же самое относится и к «входному импедансу».

В дальнейшем речь пойдет о схемах, для питания которых используется синусоидальный сигнал с определенной частотой. Анализ схем, работающих с сигналами другой формы, требует большей тщательности и предполагает использование других методов (например, метода дифференциальных уравнений или метода преобразования Фурье, при котором сигнал представляют в виде ряда синусоид). На практике эти методы редко используются.

Частотный анализ реактивных схем. Для начала рассмотрим конденсатор, на который подается синусоидальное напряжение источника питания (рис.2.16).

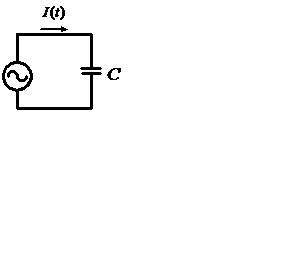
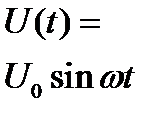
Рис.2.16. Анализ тока в цепи с конденсатором

Ток в схеме определяется следующим образом:

I(t) = C(dU /dT) = CωU₀ cosωt (2.15)

Из этого уравнения следует, что ток имеет амплитуду I и опережает входное напряжение по фазе на 90º. Если не принимать во внимание соотношение фаз, то

I(t) = 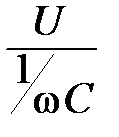(2.16)

Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением R = 1/ωC, а ток, протекающий через конденсатор, сдвинут по фазе на 90º относительно напряжения (рис.2.17).

Следует обратить внимание на то, что при прохождении синусоидального сигнала через конденсатор ток опережает по фазе напряжение, в случае с индуктивностью – ток отстает по фазе от напряжения. Для лучшего запоминания этого правила можно образно представлять, что ток «запутывается» в витках катушки индуктивности, поэтому он отстает от напряжения.

Рис.2.17. Графики тока и напряжения на конденсаторе.

Реактивное сопротивление конденсаторов и индуктивностей. Принятое соглашение позволяет применять закон Ома для схем, содержащих как резисторы, так и конденсаторы, и индуктивности. Реактивное сопротивление конденсатора равно

X_C = –j/ωC, (2.17)

Х_с – это реактивное сопротивление конденсатора на частоте ω. Для постоянного тока реактивное сопротивление равно бесконечности.

Аналогичные рассуждения для индуктивности дают следующий результат:

X_L = jωL. (2.18)

Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансом: это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на 90º – схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть. Под реактивным сопротивлением при этом подразумевается только мнимая часть импеданса.

Соглашения, принятые для представления напряжений и токов, представляют записать закон Ома в следующей простой форме:

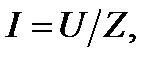
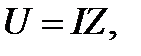(2.19)

означающий, что напряжение U, приложенное к схеме с импедансом Z, порождает ток I. Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов

Z = Z₁ + Z₂ + Z₃ +…+Z_n (2.20)

(для последовательного соединения),

Z = 1 / (1/Z₁ + 1 /Z₂ + 1/Z₃ +…+1/Z_n) (2.21)

(для параллельного соединения).

В заключение приведем формулы для определения импедансов резисторов, конденсаторов и индуктивностей:

Z_R = R – резистор,

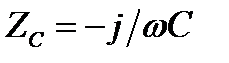– конденсатор,

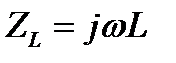– индуктивность.

Полученные зависимости позволяют анализировать любые схемы переменного тока с помощью методов, принятых для схем постоянного тока, а именно с помощью закона Ома и формул для последовательного и параллельного соединения элементов. Результаты, которые мы получили при анализе таких схем, как например, делитель напряжения, сохраняют почти такой же вид. Так же как и для схем постоянного тока для сложных разветвленных схем переменного тока справедливы законы Кирхгофа. Отличие состоит в том, что вместо токов I и напряжений U здесь следует использовать их комплексные представления: сумма падений напряжения (комплексного) в замкнутом контуре равна нулю; сумма токов (комплексных), втекающих в узел, равна сумме токов (комплексных), вытекающих из него. Из последнего правила, как и в случае с цепями постоянного тока, вытекает, что ток (комплексный) в последовательной цепи всюду одинаков.