Фильтр нижних частот (ФНЧ)

Фильтр нижних частот является схемой, которая без изменений передает сигналы нижних частот, а на высоких обеспечивает затухание сигналов и запаздывание их по фазе относительно входных сигналов. На рис.3.1 изображена схема простого RC-фильтра нижних частот.

Рис.3.1. Пассивный фильтр нижних частот

Описание в частотной области. Для расчета частотной характеристики применим формулу отношения напряжений, представленных в комплексной форме:

. (3.1)

Отсюда, учитывая, что 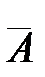=Ae^jφ, получим выражения для амплитудно–частотной характеристики (АЧХ) и фазо–частотной характеристики (ФЧХ):

. (3.2)

Обе зависимости представлены на рис. 3.2. Частота среза, на которой А= 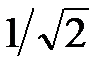, φ = –45º, определяется:

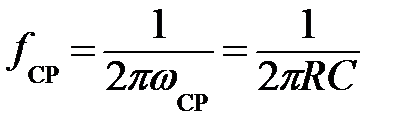. (3.3)

Как видно из рис.3.2, АЧХ наиболее просто составить из двух асимптот:

Ā = 1 = 0 дБ на нижних частотах f<<f_ср.

2) На высоких частотах f>>f_ср согласно формуле (3.2), Ā≈1/ωRC, т.е.коэффициент усиления обратно пропорционален частоте. При увеличении частоты в 10 раз коэффициент уменьшается в 10 раз, т.е. он уменьшается на 20 дБ на декаду.

Ā = 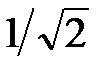= – 3дБ при f = f_ср.

Описание во временной области. Для анализа схемы во временной области подадим на вход этой схемы положительный и отрицательный скачок напряжения (рис.3.3).

Рис.3.2. АЧХ и ФЧХ фильтра нижних частот

Рис.3.3. Реакция ФНЧ на скачок напряжения

Выходные напряжения будут асимптотически приближаться к установившемся значениям U_ВЫХ = U₁ и U_ВЫХ = 0 для положительного и отрицательного скачка соответственно:

U_ВЫХ(t) = U₁(1 – e^–t/RC); (3.4)

U_ВЫХ(t) = U₁ e^–t/RC. (3.5)

В качестве меры времени установления выходного напряжения принята постоянная времени τ. Она показывает время, в течение которого процесс достигает значения, отличающегося от установившегося на 1/e часть величины скачка напряжения на входе. Из формулы (3.5) видно, что постоянная времени равна

(3.6)

Время установления выходного напряжения приближенно также можно найти из формулы (3.5).

Если в качестве входного сигнала приложено напряжение прямоугольной формы с периодом Т, то экспоненциальная функция прерывается через каждую половину периода. Какое значение при этом будет достигнуто, зависит от соотношения Т/2 и τ (рис.3.4).

Рис. 3.4. Импульсный режим работы ФНЧ при различных соотношениях частоты и постоянной времени: верхняя кривая: f_ВХ≥ 10f_СР; средняя кривая: f_ВХ = f_СР; нижняя кривая: f_ВХ≤ ¹/₁₀ f_СР

Кривые на рисунке показывают, что при увеличении постоянной времени τ наклон переходных участков увеличивается. Если постоянная времени становится достаточно большой, то на выходное напряжение цепи становится равным среднему значению входного, в ФНЧ будет работать как детектор среднего значения.

Фильтр нижних частот как интегрирующее звено. В предыдущем разделе показано, что при частотах сигнала f>>f_СР выходное переменное напряжение мало по сравнению со входным. В этом случае при |U_ВЫХ|<<|U_ВХ|, следует, что RCU_ВЫХ= U_ВХ, т.е.

(3.7)

В начале напряжение на выходе растет почти линейно, т.е. оно пропорционально интегралу входного напряжения:

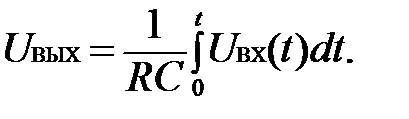(3.8)

При дальнейшем увеличении выходного напряжения ошибка увеличивается. По этой причине пассивный ФНЧ называют интегрирующей цепью. За время τ напряжение U_ВЫХ возрастает до 63%, а за время 3 τ – до 95%.Следует помнить, что ошибка интегрирования невелика лишь при t<<τ, при t=τ напряжение на выходе идеального интегратора равно U_ВХ, а на выходе RC-цепи – только 0,632U_ВХ, т.е. погрешность составляет 37%.

Длительность фронта импульса и частота среза фильтра. Другим параметром, характеризующим ФНЧ, является длительность фронта импульса. Этот параметр показывает время, в течение которого выходное напряжение возрастает от 10 до 90% конечного значения, если на вход подать импульс напряжения прямоугольной формы. Учитывая свойства экспоненциальной функции, из формулы (3.5) получим

t_Ф = t_90% – t_10% = τ(ln0,9 – ln0,1) ≈ 2,2 τ.

При f_СР = 1 / 2πτ длительность фронта импульса

t_Ф = 1 / 3f_СР. (3.9)

Это соотношение с большой долей точности действительно для фильтра нижних частот с ненагруженным выходом.