Методы исследования прохождения сигналов в электронных цепях

Методы исследования прохождения сигналов через электронные цепи основываются на основных законах электрических и электромагнитных цепей. Для применения этих законов характеристики электронных устройств линеаризуются, а электронные элементы заменяются эквивалентными схемами по постоянному и переменному току для переменных сигналов и для установившегося или переходного режимов для импульсных сигналов. Эти эквивалентные схемы представляют собой совокупность источников токов, напряжений и пассивных элементов – емкостей, индуктивностей, активных сопротивлений.

Таким образом, любую электронную схему, формирующую и преобразовывающую электрические сигналы, можно представить в виде электрической схемы и уже к ней применять известные методы, позволяющие оценить процессы в этих эквивалентных схемах, а значит, и в базовых электронных схемах, при воздействии типовых возмущений – гармонического воздействия или скачка напряжения.

1. Наиболее наглядное представление о динамических свойствах той или иной электронной схемы как звена систем автоматического управления дает так называемая переходная функция.

Переходной функцией h(t) называется изменение выходной величины во времени при поданном на вход звена единичном возмущении типа ступенчатой функции (скачка) при нулевых начальных условиях.

Переходная функция преимущественно используется для анализа импульсных сигналов и цепей, поскольку ступенчатая функция сама по себе является частью импульсного сигнала.

2. Для оценки характеристик и динамических свойств аналоговых сигналов и формирующих и преобразующих их устройств чаще используют типовое возмущение в виде единичного гармонического колебания.

В режиме вынужденных колебаний выходная величина исследуемого при таком возмущении устройства (звена) будет иметь вид

x_ВЫХ(ωt) = K(ω)e ^{j[ωt –φ(ω)]}, (1.9)

где K(ω) – амплитуда и φ(ω) – фаза колебаний на выходе устройства.

Таким образом, характеристики электронного устройства могут быть определены по его воздействию на амплитуду и фазу проходящего через него гармонического сигнала. А так как характеристики устройств, преобразующих аналоговые сигналы, линейны или близки к ним, то полученные таким образом характеристики описывают свойства исследуемых цепей и устройств и для многочастотных сигналов.

Для того чтобы определить, насколько изменятся амплитуда и фаза, необходимо выходную величину x_ВЫХ(ωt) разделить на x_ВХ(ωt).

Отношение

W(jω) = x_ВЫХ(ωt) / x_ВХ(ωt) = K(ω)e ^–jφ(ω), (1.10)

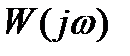представляет собой комплексное число, которое на комплексной плоскости изображается как вектор. Комплексное число называют также комплексным коэффициентом усиления. Если воспользоваться геометрической интерпретацией ), то при изменении ω от –∞ до +∞ конец вектора опишет кривую. Эту кривую называют амплитудно-фазовой частотной характеристикой.

Зависимость модуля K(ω) от частоты называют амплитудной частотной характеристикой (АЧХ), а зависимость фазы φ(ω) от частоты – фазовой частотной характеристикой (ФЧХ).

Амплитудно-фазовая частотная характеристика широко используется, прежде всего для оценки качества прохождения сигнала через аналоговые (линейные) электронные цепи, характеризуя, как эти цепи воздействуют на амплитуду и сдвиг фазы входного сигнала. Однако ее можно совместно с переходной характеристикой использовать и для оценки импульсных устройств.

Обозначим вещественную часть комплексного числа 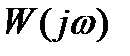через и мнимую часть – через :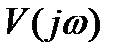

W(jω) = U(ω) + jV(ω) (1.11)

Вещественную часть комплексного числа 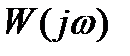называют вещественной частотной характеристикой, мнимую часть – мнимой частотной характеристикой.

Динамические характеристики электронных устройств как звеньев автоматических систем можно характеризовать также передаточной функцией.

3. Передаточной функцией звена называется отношение изображения выходной величины звена к изображению входной величины при нулевых начальных условиях

W(s) = x_ВЫХ(s) / x_ВХ(s) (1.12)

Передаточная функция устройства легко может быть получена из описывающего его эквивалентную схему уравнения, записанного в операционной форме. Например, если уравнение, описывающее эквивалентную схему устройства, имеет вид:

(Ts + 1) U(s) = KV(s) (1.13)

то его передаточная функция

W(s) = U(s) /V(s) = K / (Ts +1) (1.14)

Между передаточной функцией, амплитудно-фазовой частотной характеристикой (комплексным коэффициентом усиления), переходной функцией и дифференциальным уравнением, описывающим работу устройства, существует однозначная зависимость, поскольку они являются различными формами отражения одного и того же физического факта – преобразования воздействий, поступающих на вход устройства. Например, если дифференциальное уравнение звена имеет вид:

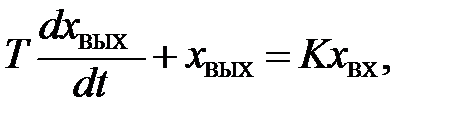(1.15)

то операционная форма записи этого уравнения при нулевых начальных условиях получается путем замены оператора дифференцирования d/dt через комплексную переменную s:

(Ts + 1)x_ВЫХ(s) = Kx_ВХ(s). (1.16)

Если входная величина представляет собой единичный скачок, то ее изображение по Карсону – Лапласу равно единице x_ВХ(s) = 1, следовательно, изображение переходной функции будет равно передаточной функции

h(s) = W(s). (1.17)

Для рассматриваемого устройства изображение переходной функции равно

h(s) = K / (Ts + 1). (1.18)

Сама переходная функция, как функция времени, будет равна

h(t) = K(1 – e^–t/T). (1.19)

Амплитудно-фазовая частотная характеристика получается из передаточной функции при замене в ней s на jω:

W(jω) = K / (Tjω + 1). (1.20)

Таким образом, динамические характеристики электронных устройств, как звеньев автоматических систем, отличаются видом и областью изменения независимой переменной.

Дифференциальное уравнение и переходная функция в качестве независимой переменной имеют время, передаточная функция – комплексную переменную s, а амплитудно-фазовая частотная характеристика – угловую частоту ω.

Решение задач, связанных с определением динамических характеристик электронных устройств, и, прежде всего работающих в линейном режиме, удобно выполнять при использовании логарифмического масштаба, так как при этом существенно упрощаются графические построения, а операции умножения и деления заменяются более простыми операциями сложения и вычитания.

Этими достоинствами логарифмического масштаба следует объяснить тот факт, что в инженерной практике широко используются логарифмические частотные характеристики. Если записать амплитудно-фазовую частотную характеристику в виде:

W(jω) = K(ω)e^–jφ(ω), (1.21)

то после логарифмирования ее получим

lnW(jω) = lnK(ω)–jφ(ω). (1.22)

Кривые lnK(ω) и φ(ω), построенные в логарифмическом масштабе частот [ln(ω)], соответственно называются амплитудной логарифмической и фазовой логарифмической частотными характеристиками.

В практике пользуются логарифмами относительных величин. При построении амплитудной логарифмической частотной характеристики по оси ординат откладывают величину L = 20lgK.

За единицу масштаба по оси по оси ординат выбирают децибел, а по оси абсцисc откладывают частоту в логарифмическом масштабе, т.е наносятся отметки, соответствующие lg(ω), а около отметок пишется само значение частоты ω в рад/с. Следует учесть, что точка ω=0 лежит на оси частот слева в бесконечности, так как lg0 = –∞. Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход амплитудной логарифмической характеристики.

Условно принимают, что при двукратном изменении частоты в логарифмическом масштабе частота изменяется на октаву, а при десятикратном – на декаду. При использовании этих единиц измерения масштабная сетка получается равномерной.

Прохождение сигналов через линейную цепь. Рассмотрим линейную цепь, на которую воздействует сигнал s(t). На выходе возникает реакция – выходной сигнал y(t) (рис.1.11).

Известно, что при воздействии на линейную цепь гармонического сигнала s(t) = S_mcos(ωt + φ_S), на выходе цепи устанавливается сигнал, форма которого тоже гармоническая: y(t) = Y_mcos(ωt + φ_Y). Гармонический сигнал – единственный сигнал, не изменяющий свою форму при прохождении через линейную электрическую цепь.

Рис.1.11. Прохождение сигнала через линейную цепь.

Пусть на линейную цепь воздействует сложный негармонический сигнал s(t). Форма сложного сигнала при прохождении через цепь будет искажаться. Для расчетов искажений выходного сигнала y(t) наиболее часто используются спектральные методы и их обобщения. Суть спектрального метода проста. Сложный сигнал с помощью рассмотренных выше спектральных разложений представляется в виде суммы гармонических колебаний. Затем находятся частичные реакции линейной цепи на каждый их гармонических входных сигналов. После этого, в соответствии с принципом суперпозиции результирующий выходной сигнал находится как сумма частичных реакций линейной цепи.

Спектральный метод анализа линейных цепей определяет два простых правила, которыми следует пользоваться при определении характера прохождения сигнала через эти цепи.

Во-первых, в зависимости от требований к форме выходного сигнала следует сравнить спектр входного сигнала и амплитудно-частотную характеристику цепи. Допустим, что требования к форме выходного сигнала достаточно высоки, тогда форма АЧХ должна быть такой, чтобы без затухания передавать все значимые гармоники входного сигнала.

Во-вторых, в результате сравнения спектра сигнала и АЧХ линейной цепи можно оценить форму выходного сигнала.

В качестве примера рассмотрим прохождение прямоугольных импульсов через фильтр нижних частот. Прямоугольный импульс формируется набором нечетных гармоник, однако за формирование фронта и среза отвечают высокие гармоники, а за формирование вершины импульса – нижние гармоники. При прохождении сигнала через фильтр высокие гармоники подавляются, следовательно, в выходном сигнале уменьшится их амплитуда. Это приведет к тому, что фронты прямоугольных импульсов будут более пологими, а вершины не изменятся.

ГЛАВА 2

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ