Основные характеристики переменных электрических сигналов
Переменный электрический сигнал в большинстве случаев представляет собой функцию времени u(t) с периодом Т = 1/f, которую можно записать в виде ряда Фурье:
u(t) = U0 + U1maxcos(ω0t–φ1) + U2maxcos(2ω0t–φ2) +
U3maxcos(3ω0t–φ3) +…, (1.8)
где ω0 = 2πƒ0;
φ1, φ2, φ3,.– начальные фазы отдельных гармоник;
U1max, U2max, U3max,… – их амплитуды.
Отдельные слагаемые суммы (1.8) называют гармониками, причем колебания основной частоты называют первой гармоникой и т.д.
Совокупность величин UКmax называют спектром амплитуд, совокупность величин φК – спектром фаз. Чаще всего интересуются только спектром амплитуд и называют его для кратности просто спектром. Графические изображения спектров даны на рис. 1.9.
Длины вертикальных отрезков представляют собой амплитуды соответствующих гармоник. Эти отрезки называют спектральными линиями, а сам спектр – линейчатым.
В общем случае сумма (1.8) является бесконечным рядом, т. е. спектр сигнала бесконечен. Так как амплитуды гармоник по мере увеличения их номера (угловой частоты ω) убывают, начиная с некоторой гармоники, высокочастотными колебаниями пренебрегают, тем самым, ограничивая спектр сигнала.
Интервал частот, в котором размещается ограниченный спектр, называется шириной спектра. Ограничение спектра производят исходя из допустимого искажения сигнала так, чтобы не потерять содержащуюся в нем информацию.
а)
б)
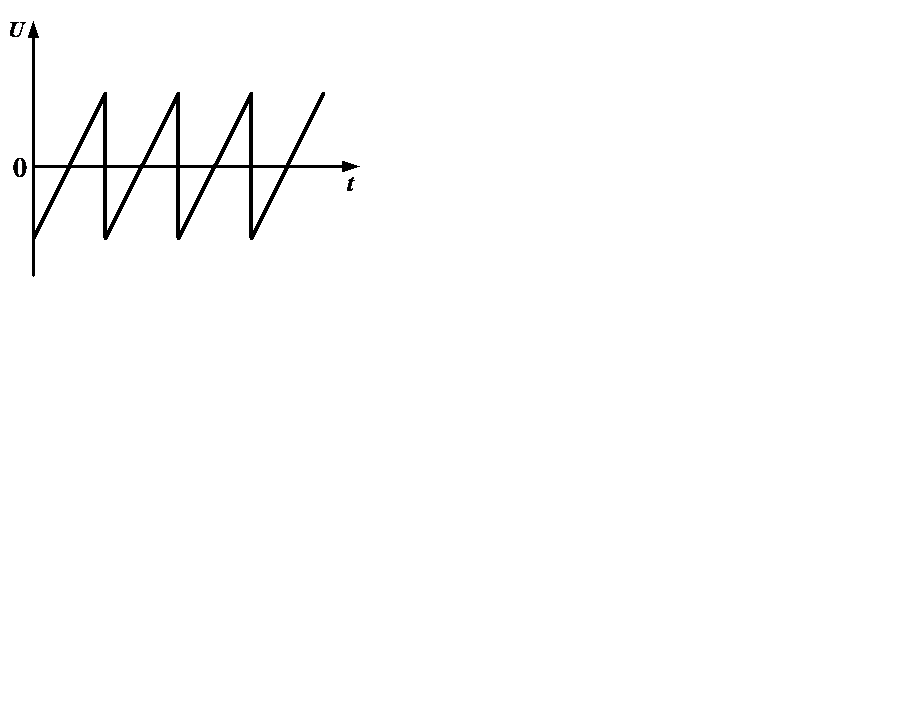
Рис.1.9. Форма сигналов и графическое изображение спектра: а) прямоугольных импульсов, б) пилообразных импульсов
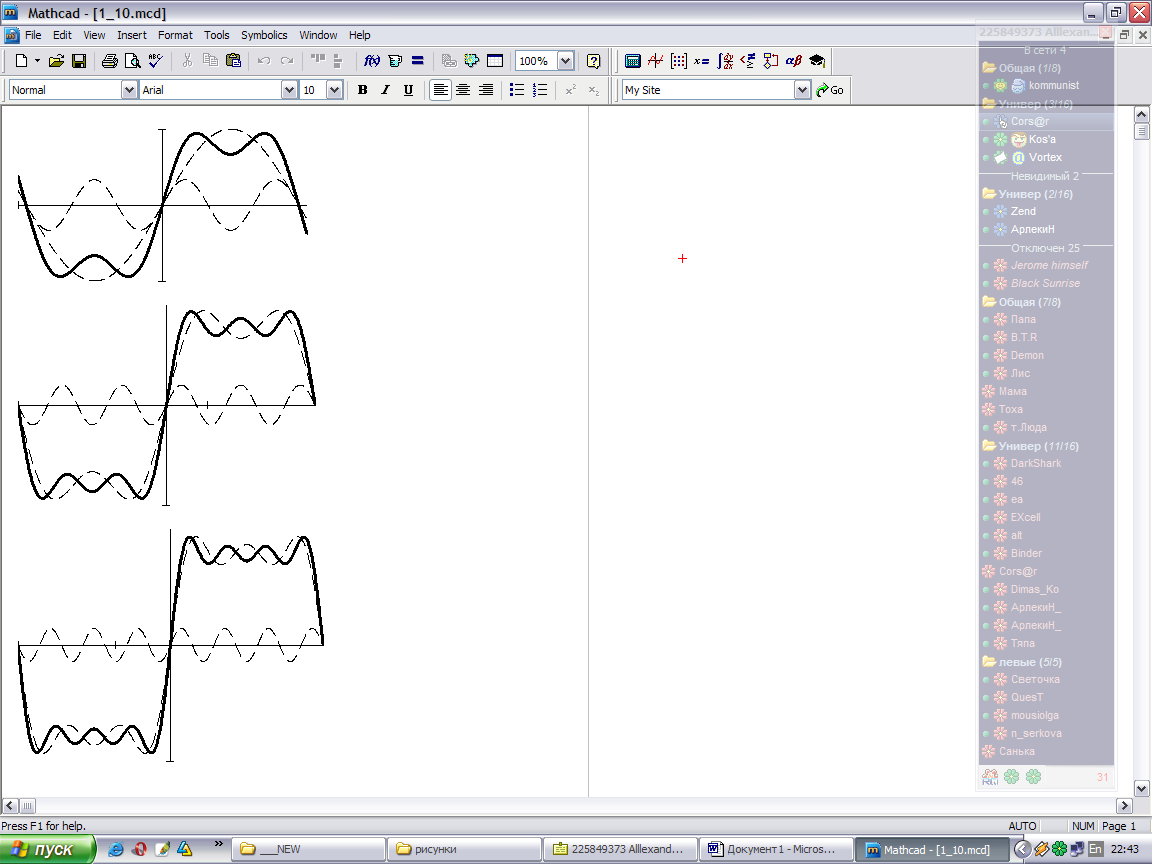
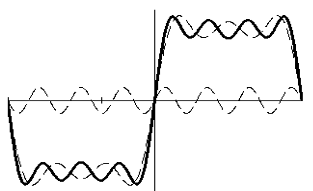
На рис.1.10 показано, как формируются прямоугольные импульсы из гармоник. Графики 1-й (n=1) и 3-й (n=3) гармоник и их суммы изображены на рис.1.10, а. На рис.1.10, б эта сумма дополнена 5-й гармоникой, а на рис.1.10, в – 7-й. Характерно, что прямоугольные импульсы, также как и треугольные, являются четными относительно t и содержат только нечетные гармоники.
Пилообразное колебание является нечетным относительно t и содержит в своем составе как четные, так и нечетные гармоники. Форма и спектр пилообразного сигнала изображены на рис.1.9, б.
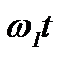
|
| E |
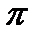
|
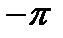
|
| 0 |
| U |
| n=1 |
| 3 |
а)
| U |
| 5 |

| 0 |
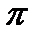
|
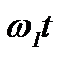
|
б)
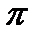
|
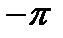
|
| 0 |
| U |
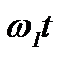
|
в)
Рис.1.10. Суммирование 1-й и 3-й гармоник (а), 1, 3 и 5-й
гармоник (б), 1, 3, 5 и 7-й гармоник (в)
прямоугольного колебания
Дата добавления: 2015-12-29; просмотров: 1464;
