Общая задача управления запасами

Постановка задачи

Допустим, что потребность предприятия в каком-либо сырье или полуфабрикате составляет Q, единиц (м³, т, шт., ...) за период Т. Поступление и расход сырья происходят равномерно, однако темп потребления несколько выше темпа поступления. Вследствие этого возникают простои предприятия из-за неудовлетворенного спроса и появляются убытки, составляющие величину Cu, приходящиеся на единицу ресурса в единицу времени. В течение времени tl и t4 каждого периода t происходит поставка материала, а во время t2 и t3 – его потребление. Однако уровень образующегося запаса при поставке сырья недостаточен для удовлетворения спроса. В течение интервала t4 запас отсутствует, при этом неудовлетворенный спрос покрывается из следующей партии. Требуется определить, какова должна быть величина поставляемой партии S и размер потребной партий V, чтобы затраты на доставку, хранение и убытки с учетом неудовлетворенного спроса были минимальными.

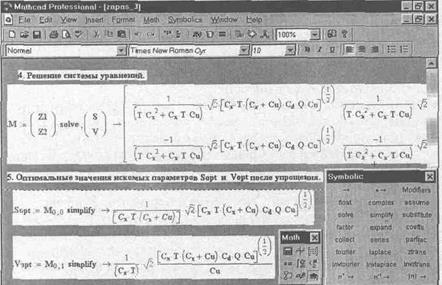
Рис. 4.3.1. Решение системы уравнений и определение

оптимальных параметров в системе Mathcad

Выявление основных особенностей, взаимосвязей и

количественных закономерностей

Обозначим через Сх затраты на хранение единицы запаса в единицу времени, а через Cd – затраты на поставку партии материалов. При этом расходы на поставку одной партии не зависят от количества материала в ней.

Графически движение запасов при неполном удовлетворении спроса представлено на рис. 7.15.

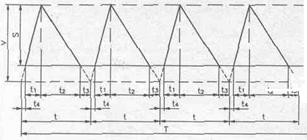
Рис. 4.3.2 График формирования и расходования

материалов при неудовлетворении спроса

По графику из подобия треугольников легко составить следующие зависимости:

(t1+t2)/t=S/V, откуда t1+t2=S×t/V;

(t3+t4)/t=(V–S)/V, откуда t3+t4=t(V–S).

Количество необходимых поставок для удовлетворения месячной потребности в материале n можно определить по формулам (nl=n2): n1=T/t; n2=Q/S.

Затраты на хранение одной партии материалов составят: Yx=(Cx S(t1+t2)/2.

Затраты на доставку одной партии материалов составят: Yd=Cd.

Убытки от недопоставки одной партии материалов: Yu=Cu(V–S)(t3+t4)/2.

Решение задачи традиционными методами

Y=Yx×n1+Yd×n2+Yu×n1=Cx×S(t1+t2)/2 ×T/t + Cd×Q/V + Cu(V–S)(t3+t4)/2 × T/2.

Суммарные затраты на хранение, доставку и потери из-за неудовлетворенного спроса за период Т будут записаны так:

Используя ранее полученные зависимости для (tl + t2) и (t3 + 14), получим:

Y=Cx×S2×T/(2×V) + Q×Cd/V + Cu(V–S)2T/(2V).

Продифференцировав целевую функцию – критерий оптимизации Y относительно искомых параметров S и V – и приравняв полученные частные производные dY/dS и dY/dV к нулю, получим:

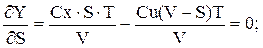
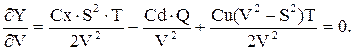
Решая систему уравнений, получим:

Sopt= 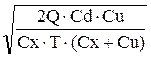, Vopt= .

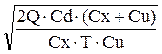Величина Сu/(Сх+Сu) называется плотностью убытков из-за неудовлетворенного спроса.