обслуживания (СМО) в неустановившемся режиме
Рассмотрим неустановившийся режим работы системы массового обслуживания, когда основные вероятностные характеристики ее зависят от некоторого промежутка времени. В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей. Таким образом, мы будем иметь систему обыкновенных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме. Для составления системы обыкновенных дифференциальных уравнений, описывающей функционирование СМО с пуассоновским потоком, существует мнемоническое правило:
• производная dPn(t)/dt вероятности пребывания системы в состоянии п равна алгебраической сумме нескольких членов;
• число членов этой суммы равно числу стрелок на графе состояний системы, соединяющих состояние n с другими;
• если стрелка направлена в рассматриваемое состояние n, то член берется со знаком «плюс»;
• если стрелка направлена из рассматриваемого состояния n, то член берется со знаком «минус»;
• каждый член суммы равен произведению вероятности того состояния, из которого направлена стрелка, на интенсивность потока событий, переводящего систему по данной стрелке.
В соответствии с размеченным графом состояний (рис. 5.1.1) эта система обыкновенных дифференциальных уравнений будет выглядеть так:
dP0(t)/dt = P1(t)μ–P0(t)mλ
dP1(t)/dt = P0(t)mλ + P2(t)μ – P1(t)(μ+(m–1)λ)
dP2(t)/dt = P1(t)(m–1)λ + P3(t)μ – P2(t)(μ+(m – 2) 1)
…………………………….
dPn(t)/dt = Pn.1(t)(m–(n–1))λ + Pn+1(t) μ – Pn(t)(μ + (m–n)λ)
…………………………….
dPm(t)/dt = Pm.1(t) λ–Pm(t)μ
Как можно заметить, требуется большая вычислительная работа для определения основных параметров функционирования комплекта машин. Можно пойти тремя путями. Первый – предварительный расчет Р0 для различных значений коэффициента использования ψ (табл. 5.2.1). Второй – применение какого-либо языка высокого уровня для решения этой задачи. Третий – использование системы Mathcad.
Таблица 5.2.1
| Коэф. | Число требований, обслуживаемых системой, – т | |||||
| загр. | ||||||
| Вероятность простоя канала обслужи5ания, ро | ||||||
| 0.04 | 0.9232 | 0.8850 | 0.8469 | 0.8090 | 0.7712 | 0.7334 |
| 0.06 | 0.8872 | 0.8313 | 0.7760 | 0,7212 | 0.6670 | 0.6134 |
| 0.08 | 0.8527 | 0.7804 | 0.7092 | 0.6394 | 0.5712 | 0.5049 |
| 0.10 | 0.8197 | 0.7321 | 0.6467 | 0.5640 | 0.4845 | 0.4090 |
| 0.12 | 0.7881 | 0.6865 | 0.5885 | 0.4952 | 0.4075 | 0.3266 |
| 0.14 | 0.7580 | 0.6435 | 0.5347 | 0.4331 | 0.3602 | 0.2577 |
| 0.16 | 0.7293 | 0.6031 | 0.4851 | 0.3775 | 0.2822 | 0.2013 |
| 0.18 | 0.7019 | 0.5652 | 0.4398 | 0.3282 | 0.2331 | 0.1561 |
| 0.20 | 0.6757 | 0.5297 | 0.3983 | 0.2849 | 0.1918 | 0.1205 |
Рассмотрим неустановившийся режим работы системы массового обслуживания, когда ее основные вероятностные характеристики зависят от времени, например в течение 0,3 часа. В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей. Таким образом, мы будем иметь систему обыкновенных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме. Для примера ограничимся рассмотрением той же самой системы, в которой обслуживаются пять требований. Интенсивность поступления одного требования на обслуживание X равна трем поступлениям в час. Интенсивность обслуживания в канале ц составляет 29 требований в час. Эта система обыкновенных дифференциальных уравнений будет выглядеть так:
dP0(t)/dt = P1(t)μ– P0(t)mλ
dP1(t)/dt = P0(t)mλ + P2(t)μ – P1(t)(μ+(m–1)λ)
dP2(t)/dt = P1(t)(m–1)λ + P3(t)μ – P2(t)(μ+(m–2)1)
…………………………….
dP4(t)/dt = P3(t)(m–3))λ + P5(t) μ–P4(t) (μ+(m–4)λ)
P5(t)/dt = P4(t) λ–P5(t)μ
На рис. 5.2.1 представлены начальные исходные данные и система дифференциальных уравнений, описывающая функционирование одноканальной замкнутой СМО при неустановившемся режиме работы
На рис 5.2.2 система дифференциальных уравнений представлена в доступном для решения виде в системе Mathcad. Здесь изображены правые части системы дифференциальных уравнений в форме вектора-столбца, каждый элемент которого определяет значение правой части соответствующего уравнения на каждом шаге интегрирования (решения), и даны начальные значения искомых параметров тоже в виде вектора-столбца. В нижней части рисунка определены начальное и конечное время интегрирования и число шагов решения системы дифференциальных уравнений.
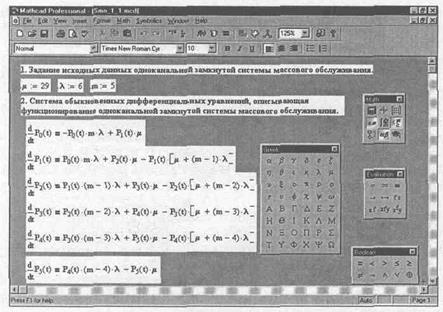
Рис 5.2.1 Описание функционирования одноканальной замкнутой системы массового обслуживания при неустановившемся режиме
На рис. 5.2.3 приведено решение системы дифференциальных уравнений одноканальной замкнутой СМО с использованием встроенной функции rkfixed(P, to,tl,N,D), реализующей метод Рунге-Кутта с фиксированным шагом. Для вызова этой функции щелкните по пункту Function (Функция) падающего меню пункта Insert (Вставка) главного меню или нажмите комбинацию клавиш Ctrl+E. Появится диалоговое окно Insert Function (Вставить функцию) В списке Function Category (Категория функции) найдите строку Differential Equation Solving (Решение дифференциального уравнения) и щелкните по ней левой кнопкой мыши. В правом поле Function Name (Имя функции) появится имя функции rkfixed. После этого щелкните по кнопке ОК.
Можно сразу найти функцию rkfixed в правом поле Function Name диалогового окна, после чего щелкнуть по ней мышью, а затем по кнопке ОК, но это займет больше времени. В обоих случаях в нижних полях диалогового окна будет дано правильное написание выбранной функции со всеми аргументами, а также краткое описание ее действий. На рис 5.2.3 приведено графическое решение системы дифференциальных уравнений для первых двух искомых параметров. Иными словами, графически представлено поведение первых двух параметров Р0 и Р1 – вероятности отсутствия требований и возможности наличия в системе одного требования соответственно в зависимости от времени протекания процесса.
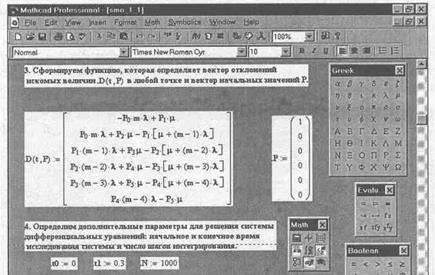
Рис 5.2.2 Описание функционирования одноканальной замкнутой СМО
при неустановившемся режиме для решения в системе Mathcad
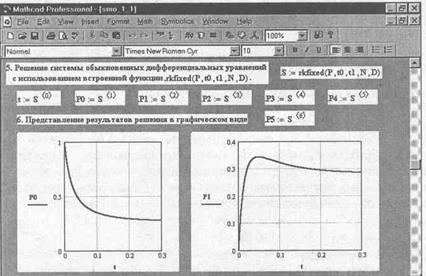
Рис 5.2.3 Результаты функционирования одноканальной замкнутой
СМО при неустановившемся режиме (начало)
На рис. 5.2.4 представлено графическое решение системы дифференциальных уравнений для остальных четырех искомых параметров. Другими словами – поведение искомых параметров Р2, Р3, Р4 и Р5 – вероятности наличия в системе двух, трех, четырех и пяти требований соответственно в зависимости от времени протекания процесса
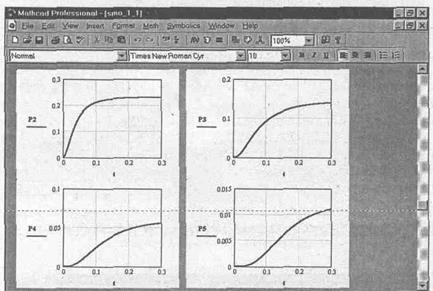
Рис. 5.2.4. Результаты функционирования одноканальной замкнутой СМО
при неустановившемся режиме в графическом виде (окончание)
Анализируя графическое решение системы обыкновенных дифференциальных уравнений, описывающей функционирование заданной одноканальной замкнутой СМО, можно заметить, что примерно через 0,3 часа система переходит в установившийся режим работы. При этом значения вероятностей состояний установившегося режима работы системы при решении совокупности обыкновенных дифференциальных уравнений практически полностью соответствуют решению системы алгебраических уравнений для установившегося режима работы:
Р0=0,271
Р1=Р0mψ=0,281
Р2=Р1 (m–1)ψ=0,233
Р3=Р2(m–2)ψ=0,144
Р4=Р3 (m – 3)ψ=0,06
Р5=Р4(m–4)ψ=0,012
На рис. 5.2.5 представлен фрагмент результатов решения системы обыкновенных дифференциальных уравнений в численном виде.
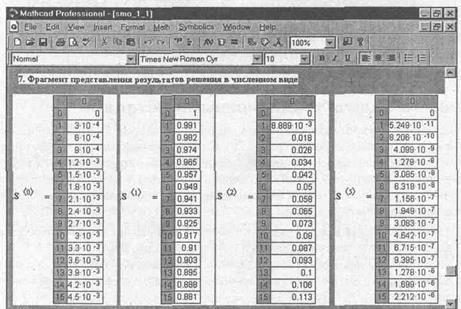
Рис 5.2.5 Фрагмент результатов решения системы обыкновенных дифференциальных уравнений в численном виде для одноканальной замкнутой СМО
Дата добавления: 2016-01-03; просмотров: 947;
