Задача управления запасами при неудовлетворении спроса
Постановка задачи
Как правило, при неудовлетворении спроса на материалы и полуфабрикаты предприятие терпит убытки, характеризующиеся величиной Си на единицу ресурса в единицу времени. На протяжении времени tl каждого периода t уровень запаса достаточен для удовлетворения спроса, а затем в течение интервала t2 запас отсутствует, причем неудовлетворенный спрос покрывается из следующей партии. Допустим, что потребность в материале составляет Q единиц за период Т. Требуется определить величину поставляемой партии S и размер потребной партии V, чтобы затраты на доставку и хранение с учетом неудовлетворенного спроса были минимальными.
Выявление основных особенностей, взаимосвязей и
количественных закономерностей
Обозначим через Сх затраты на хранение единицы ресурса в единицу времени, а через Cd – расходы на поставку партии материалов. При этом издержки на поставку одной партии не зависят от количества сырья в ней.
С помощью графика легко составить следующие зависимости:
 , откуда
, откуда 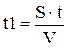 ;
;
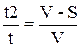 , откуда
, откуда 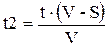 .
.
Количество поставок, необходимых для удовлетворения месячной потребности в материале n, можно определить по формулам:
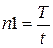 ;
; 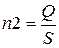 .
.
Затраты на хранение одной партии материалов составят:
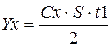 .
.
Затраты на доставку одной партии материалов составят: Yd = Cd.
Убытки от недопоставки одной партии материалов составят:
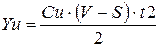 .
.
Решение задачи традиционными методами
Суммарные затраты на хранение, доставку и потери из-за неудовлетворенного спроса за период Т будут записаны так:
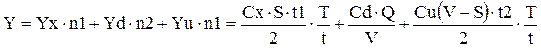 .
.
Используя ранее полученные зависимости для tl и t2, получим:
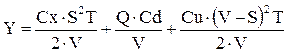 .
.
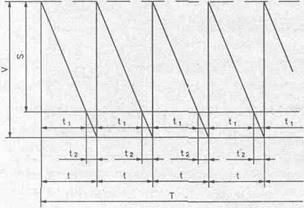
Рис. 4.2.1 График формирования и расходования запасов
материалов при неудовлетворении спроса
Продифференцировав целевую функцию (критерий оптимизации Y относительно искомых параметров S и V) и приравняв полученные частные производные dY/dS и dY/dV к нулю, получим:
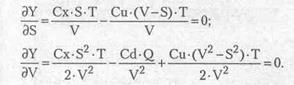
Решая систему уравнений, получим:
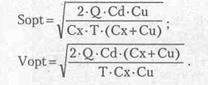
Величина Cu/(Cx+Cu) называется плотностью убытков из-за неудовлетворенного спроса.
Дата добавления: 2016-01-03; просмотров: 1091;
