Разложение сигналов в обобщенный ряд Фурье

Введем в пространстве L₂(T) базис {ψ_i(t)}. Для упрощения последующих вычислений будем полагать, что он ортонормированный, т.е. отвечает условию

.

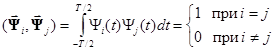Тогда любую функцию х(t) из L₂(T) можно представить через проекции C_i вектора 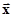на оси базиса – функции {ψ_i(t)}обобщённым рядом Фурье 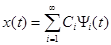. (2.1)

Для нахождения проекций C_j, называемых также коэффициентами разложения х(t) в обобщенный ряд Фурье, вычислим скалярное произведение

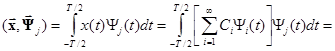
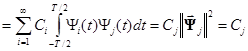
Таким образом

.

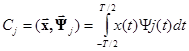Получим еще одно важное соотношение

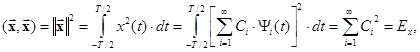являющееся частным случаем равенства Парсеваля.

Контрольные вопросы

1. Что понимают под «пространством сигналов»?

2. Какие пространства называют метрическими?

3. Что такое «метрика» пространства и каким требованиям она должна удовлетворять?

4. Какие пространства называют линейными?

5. Сформулируйте аксиомы линейного пространства.

6. Каковы условия линейной независимости векторов?

7. Что такое «линейная оболочка» векторов ?

8. Что такое «базис» в пространстве L?

9. Что называют координатами (проекциями) вектора по заданному базису?

10. Какие пространства называют нормированными?

11. Что представляет собой норма вектора и каким требованиям она должна удовлетворять?

12. Какой физический смысл имеет норма сигнала в пространствах L₂(T) и L₂(¥)?

13. Что представляет собой скалярное произведение векторов и какими свойствами оно обладает?

14. Как определяют «угол» между векторами (сигналами)?

15. Приведите примеры пространств со скалярным произведением. Как оно вычисляется в этих пространствах?

16. Как скалярное произведение порождает норму и метрику?

17. Что называют обобщённым рядом Фурье?

18. Как вычисляют коэффициенты разложения в обобщённый ряд Фурье?

19. Напишите равенство Парсеваля и дайте ему физическую трактовку.