Линейные пространства

Усовершенствуем структуру пространства сигналов, наделив его простыми алгебраическими свойствами, присущими реальным сигналам, которые можно алгебраически складывать и умножать на числа.

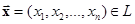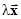ЛинейнымпространствомL над полем F называют множество элементов , называемых векторами, для которых заданы две операции –сложение элементов (векторов) и умножение векторов на элементы из поля F (называемые скалярами) . Не вдаваясь в математические детали, в дальнейшем, под полем скаляров будем понимать множества вещественных чисел R (случай действительного пространства L) или комплексных чисел С (случай комплексного пространства L). Эти операции должны удовлетворять системе аксиом линейного пространства.

1. Замкнутость операций сложения и умножения на скаляр:

,

.

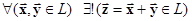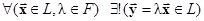2. Свойства сложения:

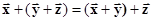ассоциативность,

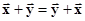коммутативность.

3. Свойства умножения на скаляр:

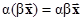ассоциативность,

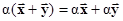дистрибутивность суммы векторов,

дистрибутивность суммы скаляров.

4. 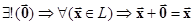существование нулевого вектора.

5. 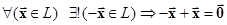существование проти-

воположного вектора.

Вектор, образованный суммированием нескольких векторов со скалярными коэффициентами

,

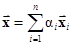называют линейной комбинацией (многообразием). Легко видеть, что множество всех линейных комбинаций векторов 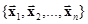при разных a_i (не затрагивая 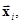) также образует линейное пространство, называемое линейной оболочкой для векторов .

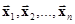Множество векторов называют линейно независимыми, если равенство

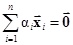
возможно лишь при всех a_i = 0. Например, на плоскости любые два неколлинеарные вектора (не лежащие на одной прямой) являются линейно независимыми.

Система линейно независимых и ненулевых векторов 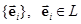образует в пространстве L базис, если

.

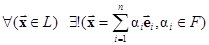Этот единственный набор скаляров {a_i}, соответствующий конкретному вектору 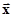, называют егокоординатами(проекциями) по базису .

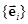Благодаря введению базиса операции над векторами превращаются в операции над числами (координатами)

.

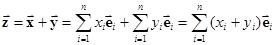Если в линейном пространстве L можно отыскать n линейно независимых векторов, а любые n + 1 векторов зависимы, то n – размерностьпространства L (dim L = n).