Пространства со скалярным произведением
Введем еще одну дополнительную геометрическую характеристику (операцию) в пространстве сигналов в виде отображения упорядоченной пары векторов на поле скаляров из F. Эту операцию называют скалярным(внутренним) произведениемвекторов и записывают в виде 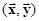 , т.е.
, т.е.
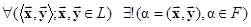 .
.
Скалярное произведение должно удовлетворять следующей системе аксиом (над полем комплексных чисел):
1) 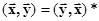 эрмитова симметрия,
эрмитова симметрия,
2) 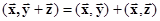 дистрибутивность,
дистрибутивность,
3) 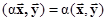 ассоциативность,
ассоциативность, 
4) 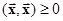 , если
, если 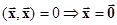 .
.
Из этих аксиом следует, что
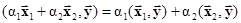 .
.
Если 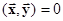 , то векторы
, то векторы 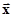 и
и 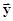 ортогональны
ортогональны  .
.
Если  (δij – символ Кронекера: δij = 1 при i = j и δij = 0 при i ≠ j), то система векторов
(δij – символ Кронекера: δij = 1 при i = j и δij = 0 при i ≠ j), то система векторов 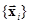 ортонормированная. Легко показать, что система ортонормированных векторов – линейно независимая.
ортонормированная. Легко показать, что система ортонормированных векторов – линейно независимая.
В линейном пространстве со скалярным произведением целесообразно норму и метрику определять через скалярное произведение
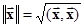 ,
,  .
.
Весьма важное значение имеет соотношение, называемое неравенством Коши-Буняковского-Шварца
 .
.
На основе скалярного произведения можно ввести понятие угла j между двумя векторами, исходя из соотношения
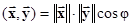 .
.
В ТЭС наибольший практический интерес представляют следующие линейные нормированные метрические пространства:
1. Rn– n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат  . Скалярное произведение векторов в этом пространстве
. Скалярное произведение векторов в этом пространстве
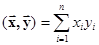 .
.
Оно порождает норму и расстояние
 ,
,
 .
.
2. L2(T) –бесконечномерные пространства (Гильберта), которое образуют непрерывные комплексные  или вещественные x(t) функции, заданные на интервале (0, Т).
или вещественные x(t) функции, заданные на интервале (0, Т).
Скалярное произведение векторов в этом пространстве
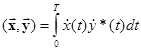 .
.
Квадрат нормы 
имеет ясный физический смысл энергии Ех сигнала, если под x(t) иметь в виду напряжение (или ток) на сопротивлении 1 Ом. Квадрат расстояния между вещественными сигналами x(t) и y(t) определяется соотношением
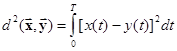
и имеет смысл энергии разностного сигнала.
3. L2(∞) – бесконечномерные пространства (Гильберта), которое образуют непрерывные комплексные  или вещественные x(t) функции, заданные на интервале (–Т/2, Т/2) при
или вещественные x(t) функции, заданные на интервале (–Т/2, Т/2) при  . Если для вещественных функций условие
. Если для вещественных функций условие

не выполняется, но выполняется условие ограничения мощности
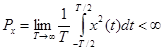 ,
,
то можно ввести скалярное произведение векторов в этом пространстве с размерностью мощности

и норму  .
.
4. 2n – n-мерное пространство Хэмминга, которые образуют двоичные n-последовательности (кодовые комбинации из 0 и 1), широко используемые в системах ПДС. Норму и метрику в этом пространстве задают в виде
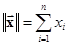 ,
,  ,
,
где знак Å обозначает операцию сложения по модулю 2 (по правилам: 0 Å 0 = 0, 0 Å 1 = 1, 1 Å 0 = 1, 1 Å 1 = 0).
Таким образом, норма вектора в пространстве Хэмминга определяется общим количеством содержащихся в нем единиц, а расстояние между двоичными векторами – количеством позиций (разрядов) кодовых комбинаций, в которых они различаются.
Следует отметить, что вещественные пространства Rn (при n → ∞), L2(T) и L2(∞) изоморфны(эквивалентны). Это означает, что между их элементами (равно как суммами элементов, их произведениями на скаляры и скалярными произведениями) можно установить взаимно-однозначное соответствие. Изоморфны также соответствующие им комплексные пространства. Понятие изоморфизма имеет большое практическое значение, так как позволяет представить одну модель сигнала другой.
Дата добавления: 2016-01-03; просмотров: 1489;
