Спектры периодических сигналов
Периодическими называют сигналы, обладающие следующим свойством
x(t) = x(t – kT), где Т – период, k = 0, ±1, ±2, ±3,… .
Как известно, такие функции (если они удовлетворяют известным из математики условиям Дирихле, которые для интересующих нас случаев всегда выполняются) можно представить суммой тригонометрического ряда (ряда Фурье)
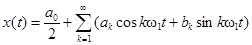 , (2.2)
, (2.2)
где 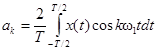 ,
, 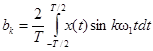 ,
,
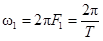 .
.
Форма (2. 1) ряда Фурье удобна с точки зрения простоты вычисления коэффициентов разложения akи bk . Ряд Фурье можно записать иначе
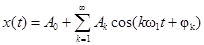 , (2.3)
, (2.3)
где 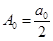 ,
, 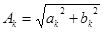 ,
, 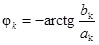 ,
,
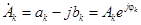 .
.
Совокупность амплитуд Ak называют амплитудным, а совокупность фаз jk – фазовым спектрами. Их можно изображать графически (рис. 2.1). Амплитудный и фазовый спектры сигнала в совокупности однозначно определяют его форму (временную зависимость).
  Ak A1 Ak A1
    A0 A2 A3 A5 A0 A2 A3 A5
  A4 A6 A7 A4 A6 A7
0 F1 2F1 3F1 4F1 5F1 6F1 7F1 f
j2 j5
Рис. 2.1. Амплитудный и фазовый спектры
|
Наиболее компактной является запись ряда Фурье в комплексной форме
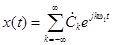 , (2.4)
, (2.4)
где 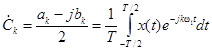 .
.
Комплексный спектр (2.4) можно интерпретировать как представление x(t) в виде сумм спектральных составляющих 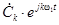 , каждая из которых представляет собой пару гармонических колебаний с половинной амплитудой
, каждая из которых представляет собой пару гармонических колебаний с половинной амплитудой 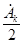 на положительной (+|k|w1) и отрицательной (–|k|w1) частотах. Для вещественных функций x(t)
на положительной (+|k|w1) и отрицательной (–|k|w1) частотах. Для вещественных функций x(t)
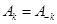 – амплитудный спектр – чётная функция частоты,
– амплитудный спектр – чётная функция частоты,
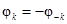 – фазовый спектр – нечётная функция частоты.
– фазовый спектр – нечётная функция частоты.
Сопоставляя (2.2) и (2.4) с (2.1), нетрудно убедиться, что ряд Фурье является частным случаем обобщённого ряда Фурье при выборе в качестве базиса совокупности тригонометрических 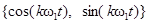 или экспоненциальных
или экспоненциальных 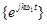 функций.
функций.
Выводы
1. Математическим аппаратом спектрального анализа периодических сигналов являются ряды Фурье.
2. Спектры периодических сигналов дискретные (линейчатые), представляют собой совокупность амплитуд и фаз гармонических колебаний (составляющих) следующих по оси частот через интервалы Δf = f1 = 1/T.
3. Ряд Фурье является частным случаем обобщенного ряда Фурье при использовании в качестве базиса
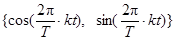 или
или 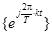 .
.
Дата добавления: 2016-01-03; просмотров: 1054;



 jk j1 j4 j6
jk j1 j4 j6 
 j3 j7
j3 j7 



 0 f
0 f