Уменьшение динамической погрешности
Целью динамических измерений является восстановление входного сигнала по зарегистрированному выходному. Выходной сигнал измерительных устройств можно найти из выражения:
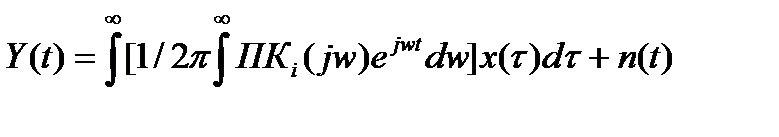 (3.98)
(3.98)
где n(t) – помеха, действующая в СИ, к – количество преобразователей; Kc(jw) – комплексная частотная характеристика преобразователей; 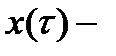 входной сигнал СИ.
входной сигнал СИ.
Из этого выражения следует, что y(t) и x(t) совпадают по форме только тогда, когда измерительное устройство обладает бесконечной полосой пропускания, а значение помехи (включая и погрешности) = 0. Так как ни то, ни другое на практике не соблюдается, возникает задача нахождения входного x(t) сигнала по известному (измеренному) выходному y(t), который относится к числу некорректных задач измерительной техники. На практике приходится находить значение x(t) по значению y(t) в условиях ограниченной полосы, точности измерения канала и действия помех в нем. Понять некорректность этой задачи проще всего в частотной области. В этом случае для динамического звена АИУ имеем:
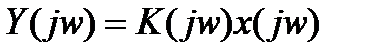 ,
,
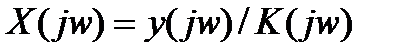 , (3.99)
, (3.99)
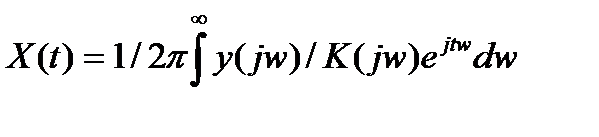 ,
,
где x(jw), y(jw) – Фурье-преобразования соответственно x(t) и y(t).
Очевидно, выражение имеет смысл только тогда, когда 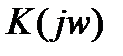 не равно 0 при
не равно 0 при 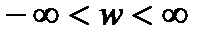 и n(t)=0. Действительно, пусть, например,
и n(t)=0. Действительно, пусть, например, 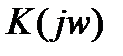 мало на участке диапазона частот
мало на участке диапазона частот 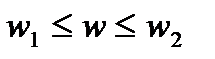 ;
;
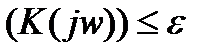 ,
, 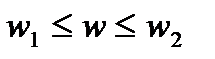 ,
, 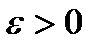 . (3.100)
. (3.100)
Тогда из спектра выходного сигнала будет “вырезан” участок в диапазоне частот 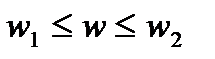 :
:
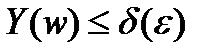 ,
, 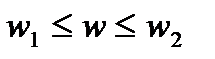 , (3.101)
, (3.101)
где 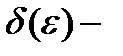 бесконечно малая величина. В этом случае уравнение (3.83) можно записать так:
бесконечно малая величина. В этом случае уравнение (3.83) можно записать так:
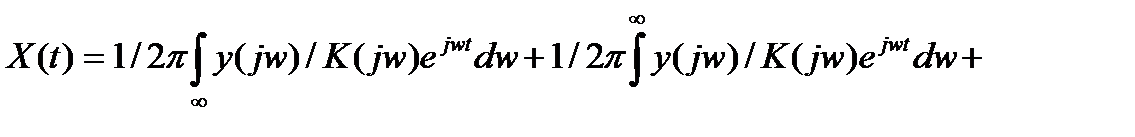 (3.102)
(3.102)
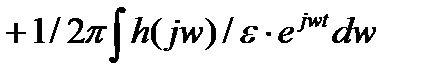
Из (3.102) видно, что даже при наличии малых помех погрешность определения x(t) может быть большой.
Если на выходе АИУ действует сигнал с финитным спектром, протяженностью 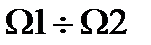 , K(jw) в этой области известен и не обращается в «0», полоса K(jw) шире полосы спектра сигнала, то
, K(jw) в этой области известен и не обращается в «0», полоса K(jw) шире полосы спектра сигнала, то
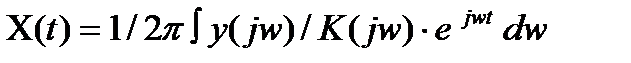 .
.
При K(jw)=1, 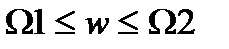 x(t)=y(t) и по значениям выходного сигнала можно однозначно определить значение входного с точностью ε. Т.к. все измерения сопровождаются погрешностью, необходимо, чтобы при:
x(t)=y(t) и по значениям выходного сигнала можно однозначно определить значение входного с точностью ε. Т.к. все измерения сопровождаются погрешностью, необходимо, чтобы при:
(y(t) – yε (t))<ε -∞<t<∞ (3.103)
(x(t) – xε(t))<η -∞<t<∞, и тогда при ε→0, η→0.
Эти условия соблюдаются для финитных функций (3.100). В этом случае измерение корректно, т.к. небольшим изменениям выходного сигнала соответствует небольшое изменение входного. Все высокие частоты в измеряемом сигнале, который, как правило, создается источниками помех, отфильтрованы. Кроме того, известно, что в идеальном АЭП K(jw)=Kном=const, φ(w) = – t3w. В таком АИУ передаточная характеристика Kном(S) не имеет нулей в правой полуплоскости комплексных переменных. Эта K(S) является передаточной характеристикой минимально-фазового типа. Для нее, если K(jw)=Kном=const, то φ(w) может быть получено из K(jw) посредством преобразования Гильберта и при этом не будет вызывать искажений измеряемой величины.
| кКЛK1(S) |
| K2(S) |
Рис. 3.14 Последовательное включение корректирующих устройств
В соответствии с этим способом коррекции последовательно со средством измерения включается корректирующий преобразователь (см. рисунке 3.14). Здесь K1(S), K2(S) – передаточные характеристики корректируемого СИ и корректирующего преобразователя. Результирующая передаточная характеристика такого соединения:
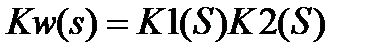 . (3.104)
. (3.104)
Если
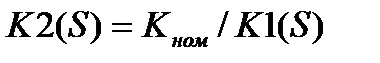 , то
, то 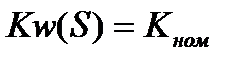 (3.105)
(3.105)
и СИ не будет иметь динамические погрешности. При этом необходимо, чтобы скорректированное СИ было бы физически осуществимо и устойчиво. Учитывая это, необходимо искать передаточную характеристику корректирующего преобразователя для СИ, имеющего K(S) минимально-фазового типа в виде:
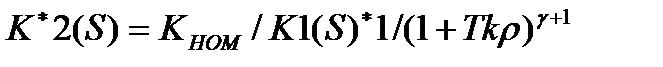 (3.106)
(3.106)
где 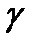 выбирается так, чтобы у
выбирается так, чтобы у 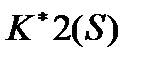 число нулей не превышало число полюсов. Очевидно, что при постоянном времени корректирующего звена
число нулей не превышало число полюсов. Очевидно, что при постоянном времени корректирующего звена 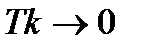 коррекция приближается к идеальной.
коррекция приближается к идеальной.
Если передаточная характеристика K1(S) СИ не минимально-фазового типа, то K1(S) имеет нули в правой полуплоскости и в соответствии с (3.96) инверсная система неустойчива, так как в ней есть полюсы, расположенные в правой полуплоскости. Для получения устойчивой работы СИ с коррекцией, необходимо в него вводить дополнительные цепи вида:
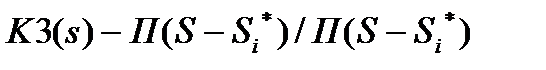 , (3.107)
, (3.107)
где 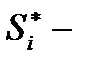 нули, лежащие в правой полуплоскости:
нули, лежащие в правой полуплоскости: 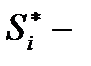 сопряженное с
сопряженное с 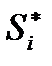 комплексное число; К – число нулей в правой полуплоскости. Такое звено не искажает АЧХ скорректированного СИ. Корректирующий преобразователь в этом случае имеет передаточную характеристику вида:
комплексное число; К – число нулей в правой полуплоскости. Такое звено не искажает АЧХ скорректированного СИ. Корректирующий преобразователь в этом случае имеет передаточную характеристику вида:
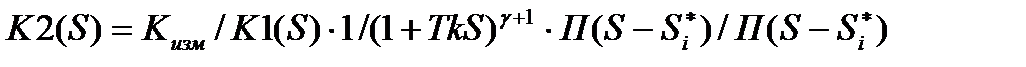 (3.108)
(3.108)
Результирующая передаточная функция СИ:
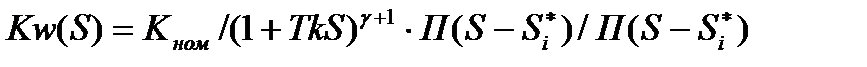 (3.109)
(3.109)
Из (3.109) видно, что скорректированное СИ имеет идеальную амплитудно-частотную (при Тк→0) и неидеальную фазочастотную характеристики. Для того чтобы в рабочем диапазоне ее приблизить к идеальной, необходимо предусмотреть еще дополнительные фазокорректирующие цепи и получить фазовую характеристику вида 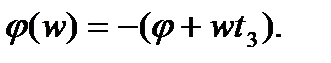 Найти соответствующую цепь – значит решить задачу синтеза оптимального СИ.
Найти соответствующую цепь – значит решить задачу синтеза оптимального СИ.
Коррекция с помощью цепи ОС.Для средства измерения, охваченного цепью ООС (рис. 3.15), можно записать:
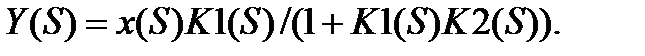 (3.110)
(3.110)
| K1(S) |
| K2(S) |
Рис.3.15. Средство измерения охваченное ООС
Для работы диапазона частот 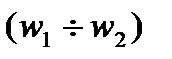 имеем:
имеем:
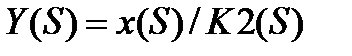 (3.111)
(3.111)
И если для 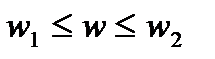 ,
, 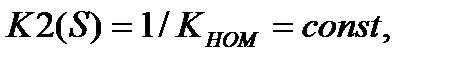 то
то 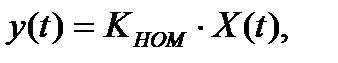
Где кном – статический номинальный коэффициент преобразования си.
Это соотношение показывает, что си с ос можно рассматривать как си с последовательной корректирующей цепью, имеющей передаточную характеристику вида 1) k2(s). Это должна быть физически реализуемая и устойчивая цепь. Требование устойчивости этого контура накладывает на него ограничения, которые были рассмотрены ранее для си с последовательной коррекцией.
Корректирование с помощью аналоговых и цифровых вычислительных устройств. Для реализации условий корректировки можно использовать вычислительную технику. Если соответствующее вычислительное устройство уже имеется в си, то корректирование можно осуществить программным способом, без дополнительных аппаратурных затрат. Если средств вычислительной техники в си нет, то корректирующие цепи целесообразно строить на базе ОУ. Используя r- и c- элементы и о.с. В усилителях, удается в достаточно широком частотном диапазоне «обменять» большое усиление ОУ не различные свойства и характеристики цепи. Для использования средств ВТ необходимо вначале произвести аналогово-цифровое преобразование выходного сигнала АИУ, а затем программными средствами корректирование его характеристик. При этом не исчезнут проблемы физической реализуемости и устойчивости, т.к. Иначе невозможно создать реализуемые программные работы ЭВМ.
Пределы корректирования. В АИУ присутствуют помехи, действие которых увеличивается с расширением полосы пропускания. Ограничением является также условие физической реализуемости корректирующего преобразователя. Существенные ограничения вносят нелинейности преобразователей и усиления параметрических влияний в скорректированном приборе. Улучшать динамические характеристики таким путем можно тогда, когда в АИУ есть «запас» по значению общей погрешности измерений в конкретных условий эксплуатации.
Выбирать оптимальные параметры коррекции необходимо путем отыскания минимума общей погрешности динамической СИ:
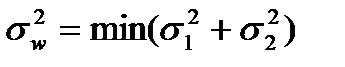 , (3.112)
, (3.112)
где σ12, σ22 – дисперсия динамической погрешности и погрешности от действия помех.
Дата добавления: 2015-12-29; просмотров: 758;
