Коррекция погрешностей
Снижение погрешности АИУ этим способом основано на выполнении вспомогательных операций в процессе измерения, что требует наличия избыточности в АИУ по быстродействию. Операция коррекции погрешностей может осуществляться автоматически или вручную. Известно много способов коррекции погрешностей: калибровка, аддитивная и мультипликативная коррекция, введение поправок, самонастройка, итерации, адаптации, способ образцовых сигналов.
наиболее часто применяются на практике следующие способы.
Калибровка.Выходной сигнал устройства, имеющего аддитивную и мультипликативную погрешности можно записать в виде:
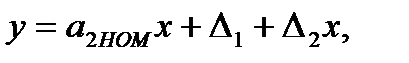 (3.48)
(3.48)
где 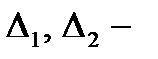 аддитивная и мультипликативная погрешности .
аддитивная и мультипликативная погрешности .
Для осуществления калибровки необходимо иметь дополнительный источник образцового сигнала или прецизионный делитель напряжения. Структурная схема устройства с образцовым источником сигнала показана на рисунке 3.6.
Здесь И0 – источник образцовых сигналов;
БУ – блок управления;
СС – схема сравнения;
SA1, SA¢1 – переключатель рода работы.
В положении 2 SA1, SA¢1 осуществляется калибровка . В это время на вход основной цепи СИ и схемы сравнения СС подается нулевой сигнал. Тогда:
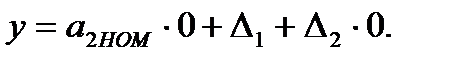 (3.49)
(3.49)
| СИ |
1 1
| СС |
| БУ |
0
| И0 |
y0
Рис. 3.6. Структурная схема цепи с образцовым источником сигнала
Здесь И0 – источник образцовых сигналов;
БУ – блок управления;
СС – схема сравнения;
SA1, SA¢1 – переключатель рода работы.
В положении 2 SA1, SA¢1 осуществляется калибровка. В это время на вход СИ и схемы сравнения СС подается нулевой сигнал. Тогда:
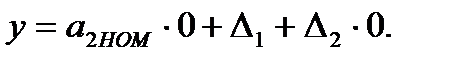 (3.50)
(3.50)
При наличии аддитивной погрешности Δ1 блок БУ измеряет параметры СИ (или выходной сигнал), устраняя эту погрешность установлением нулевого выходного сигнала СИ, и
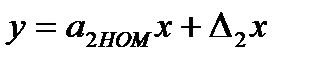 . (3.51)
. (3.51)
Затем на вход СИ подается сигнал x0, а на вход схемы сравнения сигнал y0, соответствующий этому входному сигналу в идеальном СИ. Тогда:
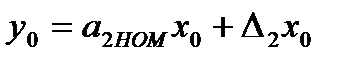 (3.52)
(3.52)
Далее с помощью БУ (или вручную) регулируется передаточный коэффициент СИ до величины 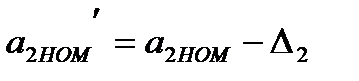 путем установления на выходе сигнала, равного y0. Затем переключатель SA1, SA¢1 переводится в положение 1 и на вход СИ поступает измеряемый сигнал. В этом случае выходной сигнал в статике
путем установления на выходе сигнала, равного y0. Затем переключатель SA1, SA¢1 переводится в положение 1 и на вход СИ поступает измеряемый сигнал. В этом случае выходной сигнал в статике
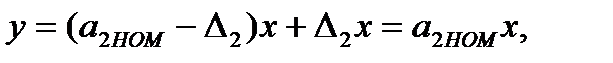 (3.53)
(3.53)
будет равен выходному сигналу идеального СИ с точностью до погрешностей калибровки. В общем случае относительная погрешность калибровки СИ состоит из следующих составляющих:
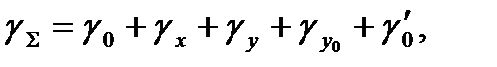 (3.54)
(3.54)
где 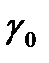 ,
, 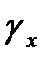 – погрешности источника образцовых сигналов;
– погрешности источника образцовых сигналов; 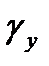 ,
, 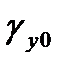 – погрешность установки чувствительности и нуля;
– погрешность установки чувствительности и нуля; 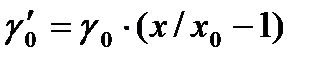 – погрешность калибровки, появившаяся из-за неполного устранения аддитивной погрешности.
– погрешность калибровки, появившаяся из-за неполного устранения аддитивной погрешности.
Если входным и выходным сигналом СИ является напряжение, то необходимость в образцовом источнике напряжения отпадает, если калибровку осуществить в соответствии со структурной схемой, показанной на рисунке 3.7.
| АЭП |
SA1 1
| F |
UK
R1 R2
Рис. 3.7. Структурная схема.
В положении 2 SA1, регулируя чувствительность, добиваются равенства показаний прибора при обоих положениях переключателя SA2. При этом передаточный коэффициент СИ устанавливают равным обратному значению коэффициента передачи делителя напряжения R1, R2. Этот способ снижения погрешностей эффективен при условии неизменности характеристик АИУ между двумя соседними калибровками и одинаковости свойств входного и калиброванного сигналов. Поэтому на практике он применяется для снижения для снижения низкочастотных составляющих погрешности АИУ, нормированная автокорреляционная функция которых 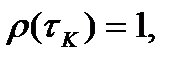 где
где 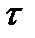 – интервал между двумя калибровками.
– интервал между двумя калибровками.
Аддитивная коррекция.При аддитивной коррекции погрешностей СИ снижение погрешности осуществляется за счёт смещения функции преобразования СИ. Для выявления погрешности, как правило, используется обратный образцовый преобразователь ОП изображенный на рисунке 3.8.
| – |
| СИ |
| – |
| ОП |
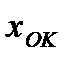 y2
y2
| ВК |
Рис. 3.8. Обратный образцовый преобразователь
Операция выделения сигнала погрешности Δx происходит в результате одновременного или разновременного вычитания двух сигналов – входного x и обратного 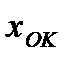 преобразователей. Усиленный вспомогательным каналом ВК разностный сигнал y2 используется для введения поправки в средство измерения. Пусть СИ имеет аддитивную и мультипликативную погрешности, и его выходной сигнал
преобразователей. Усиленный вспомогательным каналом ВК разностный сигнал y2 используется для введения поправки в средство измерения. Пусть СИ имеет аддитивную и мультипликативную погрешности, и его выходной сигнал
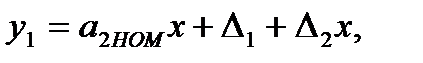 (3.55)
(3.55)
а обратный образцовый преобразователь имеет идеальную передаточную характеристику вида:
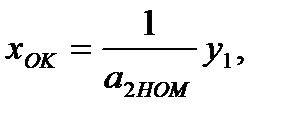 (3.56)
(3.56)
тогда
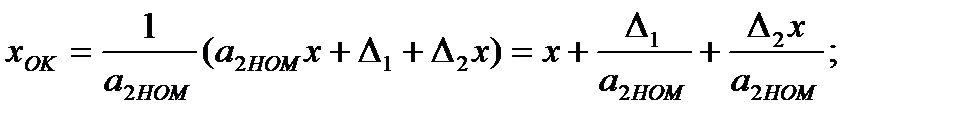 (3.57)
(3.57)
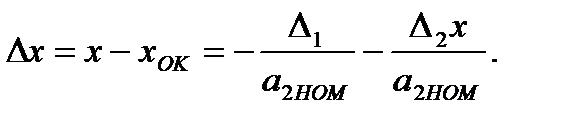
Пусть
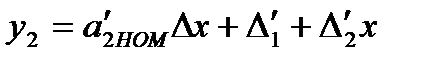 (3.58)
(3.58)
ВК имеет такие же составляющие погрешности, как и корректируемое СИ. Подставив в выражение (3.41) значение Δx, получим
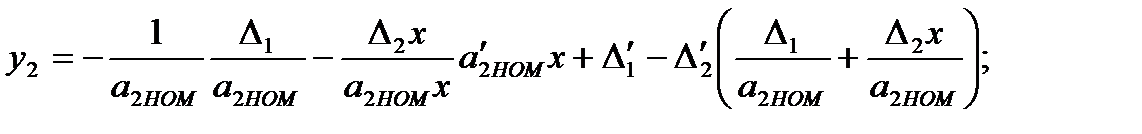 (3.59)
(3.59)
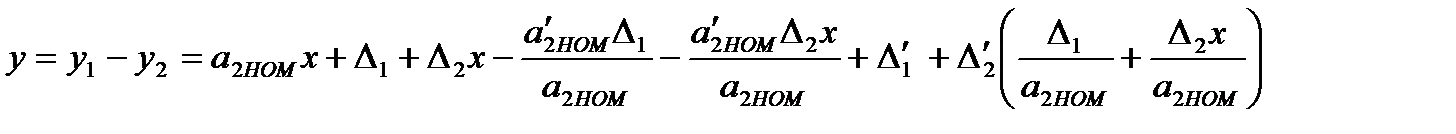 (3.60)
(3.60)
Из выражения (3.61) видно, что для получения малой остаточной погрешности скорректированного СИ необходимо иметь малую аддитивную погрешность блока ВК и равенство номинальных передаточных коэффициентов блока ВК и СИ. В этом случае 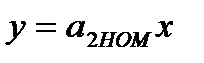 и в СИ осуществлена полная коррекция погрешностей. В общем случае погрешность скорректированного СИ зависит от значений сигнала x, то есть идеальная коррекция возможна только в одной точке шкалы СИ.
и в СИ осуществлена полная коррекция погрешностей. В общем случае погрешность скорректированного СИ зависит от значений сигнала x, то есть идеальная коррекция возможна только в одной точке шкалы СИ.
Вариант структурной схемы СИ с аддитивной коррекцией, содержащей замкнутый контур со вспомогательным каналом, показан на рисунке 3.9.
| СИ |
| – |
| – |
| ВК |
| ОП |
Рис.3.9. Вариант структурной схемы СИ
Для такой структуры имеем
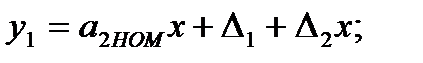
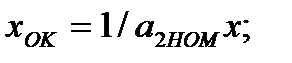 (3.61)
(3.61)
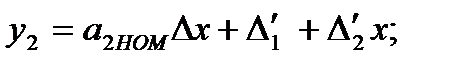
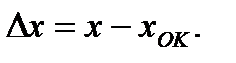
Из этих выражений несложно получить значение выходного сигнала:
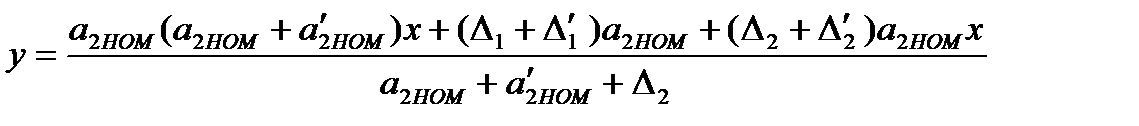 . (3.62)
. (3.62)
Так как 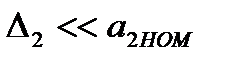 , то
, то
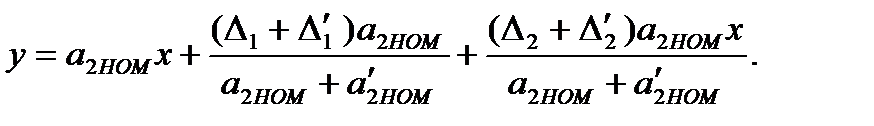 (3.63)
(3.63)
При 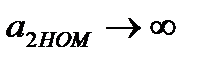 имеем
имеем 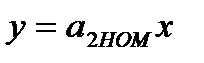 , а стабильность передаточного коэффициента блока ВК не сказывается на работе устройства. Однако в состав СИ входит замкнутый контур, и, следовательно, увеличение
, а стабильность передаточного коэффициента блока ВК не сказывается на работе устройства. Однако в состав СИ входит замкнутый контур, и, следовательно, увеличение 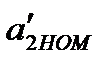 ограничено условиями устойчивости работы СИ. Но так как процесс погрешности более медленный, чем входной сигнал, то ВК может быть выполнен узкополосным.
ограничено условиями устойчивости работы СИ. Но так как процесс погрешности более медленный, чем входной сигнал, то ВК может быть выполнен узкополосным.
Мультипликативная коррекция. В схеме с мультипликативной коррекцией погрешностей осуществляется выделение погрешности СИ и управление ею с помощью коэффициента преобразования СИ для миниминизации этой погрешности. Таким способом можно корректировать аддитивную и мультипликативную погрешности. Для аддитивной погрешности коррекция осуществляется лишь в одной точке шкалы.
| СИ |
z
| – |
| ВК |
| ОП |
Рис. 3.10.Структурная схема с мультипликативной коррекцией
Пусть характеристика преобразования такого СИ имеет вид:
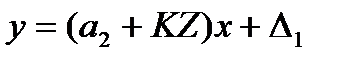 , (3.64)
, (3.64)
где KZ – изменение коэффициента преобразования СИ от действия сигнала Z; Δ1 – аддитивная погрешность. Запишем:
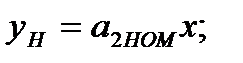
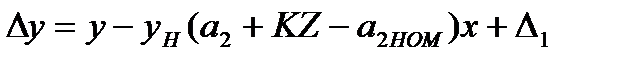 ;
;
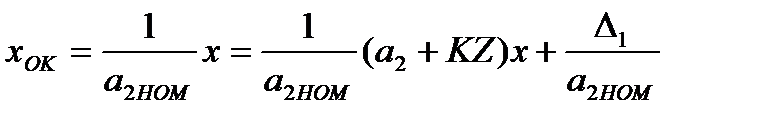 ; (3.65)
; (3.65)
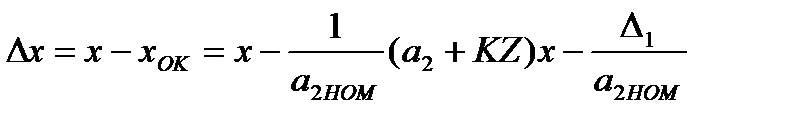 ;
;
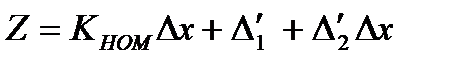 ,
,
где 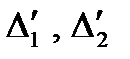 – аддитивная и мультипликативная погрешности блока ВК.
– аддитивная и мультипликативная погрешности блока ВК.
Подставив в выражение для Z значение Δx, получим выражение, определяющее вид выходного сигнала блока ВК. Тогда:
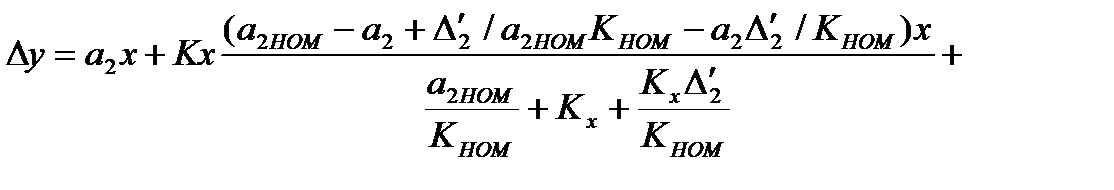
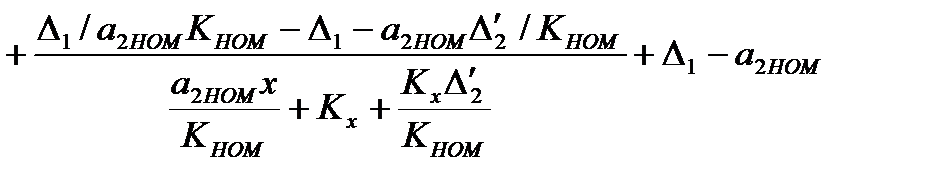 (3.66)
(3.66)
Из этого соотношения видно, что для снижения погрешности СИ необходимо повысить коэффициент передачи вспомогательного канала ВК. При КНОМ → ∞ имеем ∆y = 0. В общем случае значение погрешности скорректированного СИ ∆y зависит от значения x, поэтому для хорошей коррекции погрешности таким способом все указанные соотношения должны выполняться во всем частотном диапазоне измерения входной величины. При наличии в СИ только мультипликативной погрешности требования к быстродействию блока ВК могут быть снижены за счёт придания замкнутому контуру свойств астатизма, для чего в состав ВК должно быть введено интегрирующее звено.
Автоматическая коррекция погрешностей способом итераций. Использование этого способа в ряде случаев позволяет свести точность измерения с помощью АИУ к точности используемой образцовой меры. Этот способ требует наличия избыточности СИ по быстродействию, а для своей реализации и структуру избыточности.
Принципиально возможно построение таких структур с временным и пространственным разделением каналов. Структурная схема СИ с временным
разделением каналов показана на рис. 3.11.
| СИ |
| ВУ |
1 y y
| ОП |
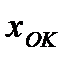
Рис. 3.11. Структурная схема СИ с временным разделением каналов
Здесь ВУ – вычислительное устройство; ОП – обратный преобразователь. В положении 1 SA1 осуществляется измерение входной величины x, а положении 2 SA1 – измерение выходного сигнала ОП 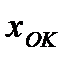 .
.
Пусть 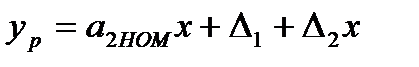 и результатом первого измерения x будет величина
и результатом первого измерения x будет величина
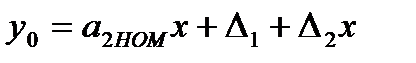 (3.67)
(3.67)
Результат первого обратного преобразования в этом случае можно записать в виде:
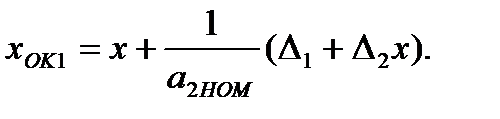 (3.68)
(3.68)
После измерения значения 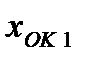 , получим:
, получим:
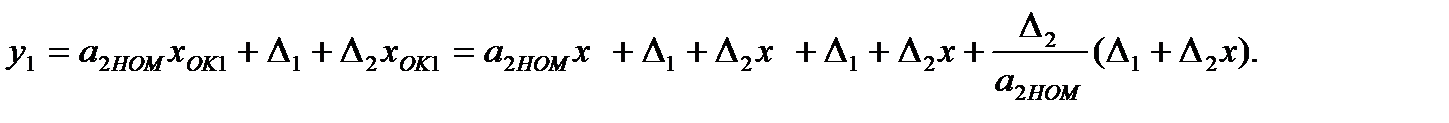 (3.69)
(3.69)
В вычислительном устройстве ВУ вычисляется разность первого и второго измерений:
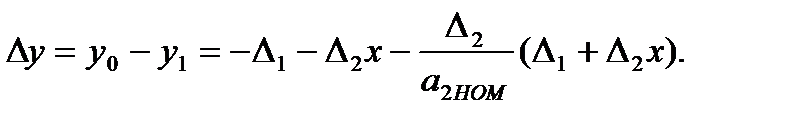 (3.70)
(3.70)
Эта разность запоминается в ВУ и переключатель SA1 снова подключает на вход СИ измеряемое значение х. Тогда:
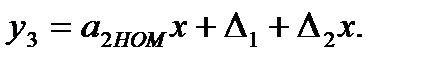 (3.71)
(3.71)
Записав таким образом результат следующего измерения х, предположим, что процесс погрешностей ∆1, ∆2 низкочастотен, и за время итераций ∆1 ≈ const, ∆2 ≈ const.
После получения значения у3 вносим в результат измерения первую поправку (1-я итерация). Получаем:
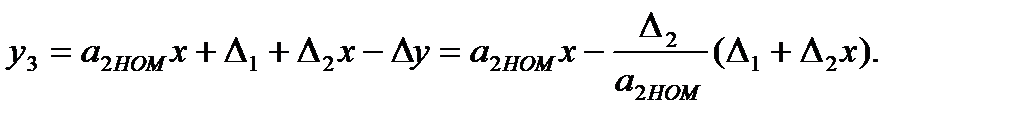 (3.72)
(3.72)
Так как  , то процесс итераций сходится. Далее повторяем процесс итераций – снова преобразуем в ОП результат следующего измерения у3. Имеем:
, то процесс итераций сходится. Далее повторяем процесс итераций – снова преобразуем в ОП результат следующего измерения у3. Имеем:
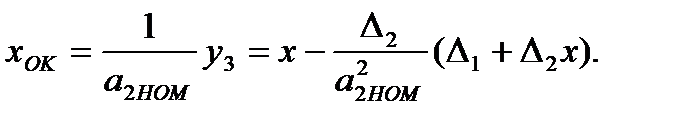 (3.73)
(3.73)
Измеряем 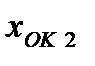 :
:
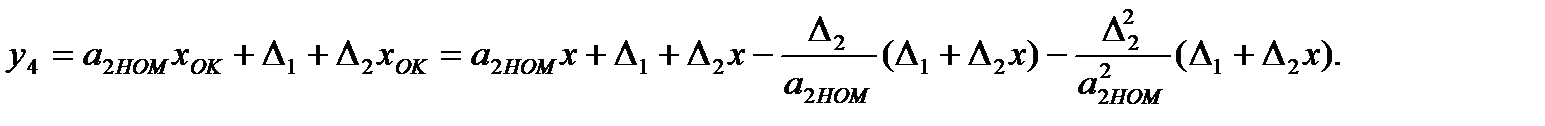 (3.74)
(3.74)
Вычисляем вторую поправку и запоминаем ее а ВУ:
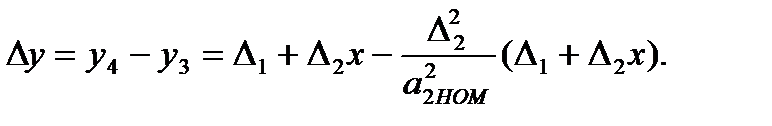
Снова измеряем х и вносим вторую поправку (2-я итерация):
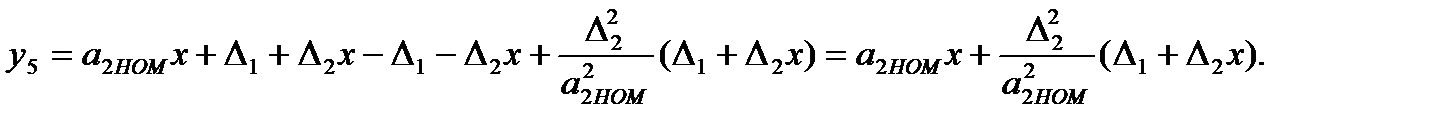 (3.75)
(3.75)
После окончания n итераций имеем результат измерений в виде:
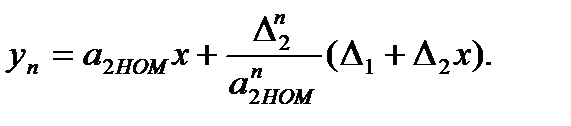 (3.76)
(3.76)
откуда видно, что при 
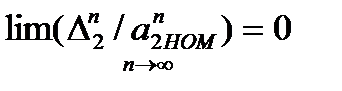 и
и
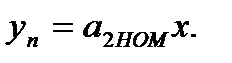 (3.77)
(3.77)
В реальном случае не удастся получить такой результат, так как на точность работы СИ влияет точность выполнения операций вычитания и запоминания в ВУ и погрешности ОП. Необходимо также отметить, что все высокочастотные составляющие погрешности такого СИ могут увеличиться, так как в ВУ осуществляется много операций вычитания, дисперсия разности некоррелированных величин равна сумме дисперсий слагаемых. Поэтому способ итераций применяется для снижения коррелированной составляющей погрешности в АИУ. При пространственном разделении каналов отключение измерительной величины от АИУ не требуется, но для построения такого АИУ требуется несколько одинаковых прямых и обратных образцовых преобразователей. Структурная схема такого СИ показана на рисунке 3.12.
Y1 Y2 Yn Y
Y2¢ Yn¢
| ОП1 |
| ОП2 |
| ППn |
| ПП2 |
| ПП1 |
ΔX1 ΔX2 ΔXn
X
Рис. 3.12. Структурная схема СИ с пространственным разделением каналов
Если все прямые и обратные преобразователи одинаковы, то для такой структурной схемы можно записать:
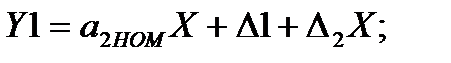
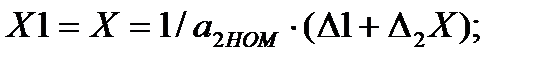
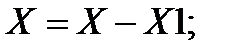 (3.78)
(3.78)
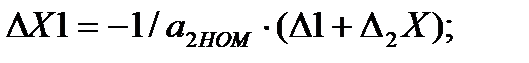
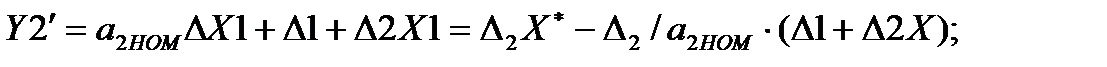 (3.79)
(3.79)
 (3.80)
(3.80)

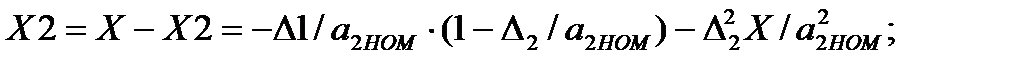 (3.81)
(3.81)
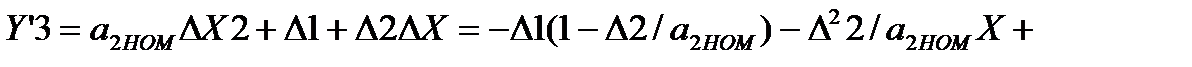
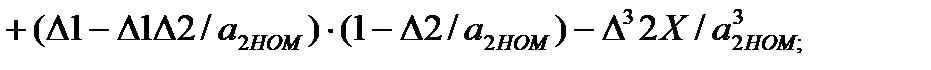 (3.82)
(3.82)
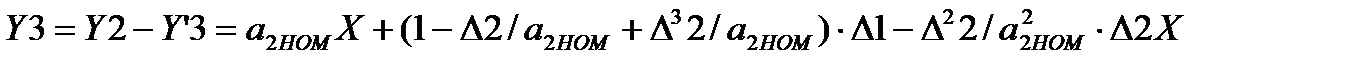
Так как  , то
, то 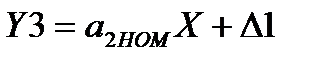 , и погрешность СИ определяется практически аддитивной погрешностью последовательного преобразователя в установке.
, и погрешность СИ определяется практически аддитивной погрешностью последовательного преобразователя в установке.
Способ образцовых сигналов.Для практической реализации способов повышения точности СИ необходимо иметь избыточность по быстродействию и набор образцовым сигналов. Структурная схема подобной СИ показана на рисунке 3.13.
| Р |
| СИ |
| ВУ |
Рис. 3.13. Структурная схема СИ с набором образцовых сигналов
Здесь Р – распределитель, включающий поочередно к входу СИ измеряемое значение Х и образцовые сигналы Х01, Х02; ВУ – вычислительное устройство. В случае линейной СИ можно записать для первого, второго и третьего измерений соответственно:
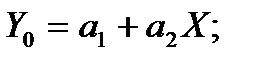
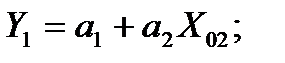
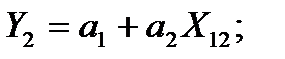 (3.83)
(3.83)
где 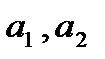 – коэффициенты характеристики преобразования СИ. Решив эту систему уравнений, можно найти значение входной величины:
– коэффициенты характеристики преобразования СИ. Решив эту систему уравнений, можно найти значение входной величины:
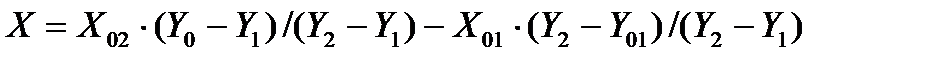 . (3.84)
. (3.84)
Как видно из этого выражения, значение Х не зависит от изменяющихся параметров характеристики преобразования. Таким способом уменьшают значение как аддитивной, так и мультипликативной составляющих погрешностей СИ. Это дает хорошие результаты, когда значения коэффициентов 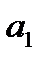 и
и 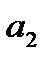 не изменяются за время, необходимое для получения одного результата измерения. Кроме того, процесс измерения прерывается, что приводит в АИУ к возникновению погрешности дискретности. Остаточная погрешность скорректированного АИУ определяется измерениями коэффициентов характеристики преобразования и сигнала между двумя коррекциями, адекватностью реального входного сигнала и образцовых сигналов, инструментальными погрешностями всего устройства и отличием реальной статистической преобразования от записанной в ВУ. Этот способ позволяет скорректировать погрешности нелинейного СИ, но и в этом случае в ВУ придется решать систему уравнений со многими неизвестными.
не изменяются за время, необходимое для получения одного результата измерения. Кроме того, процесс измерения прерывается, что приводит в АИУ к возникновению погрешности дискретности. Остаточная погрешность скорректированного АИУ определяется измерениями коэффициентов характеристики преобразования и сигнала между двумя коррекциями, адекватностью реального входного сигнала и образцовых сигналов, инструментальными погрешностями всего устройства и отличием реальной статистической преобразования от записанной в ВУ. Этот способ позволяет скорректировать погрешности нелинейного СИ, но и в этом случае в ВУ придется решать систему уравнений со многими неизвестными.
Дата добавления: 2015-12-29; просмотров: 1702;
