Компенсация погрешностей

В аналоговых измерительных устройствах применяется компенсация погрешностей способом составляющих параметров и компенсирующего преобразования с полной и неполной компенсацией. Наиболее широко применяется способ составляющих параметров. Этот способ, в отличие от способа ООС, не является универсальным, так как для уменьшения действия каждого влияющего фактора в АИУ необходимо вводить отдельно дополнительные элементы, уменьшающие влияние только одного конкретного фактора на работу прибора.

Рассмотрим этот способ на примере уменьшения погрешности АИУ, вызванной изменением некоторого влияющего фактора ξ. Пусть изменение этого фактора вызывает в АИУ появление погрешности Δξ с математическим ожиданием m[Δξ] и дисперсией σ²[Δξ]. Рассмотрим процесс компенсации случайной составляющей погрешности σ[Δξ], так как компенсацию систематической погрешности этим методом можно рассматривать как частный случай компенсации случайной погрешности. В соответствии с данным способом в схему АИУ включается некоторый элемент, вызывающий в АИУ появление погрешности Δ_К(ξ), коррелированной с погрешностью Δξ, и имеющей плотность распределения, близкую к плотности распределения погрешности Δξ прибора. Значение остаточной погрешности Δ_К(ξ) в этом случае можно определить из формулы:

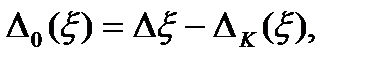(3.44)

Дисперсия остаточной погрешности:

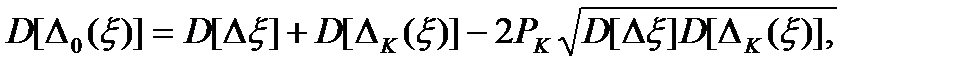(3.45)

где Р_К – нормированный коэффициент корреляции погрешностей Δξ и Δ_К(ξ).

Из (3.46) найдем оптимальное значение 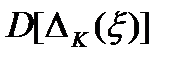, минимизирующее значение остаточной погрешности. Для этого определим производную от 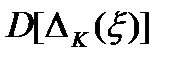и приравняем ее нулю. Тогда оптимальное значение:

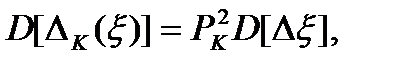(3.46)

а минимальное значение

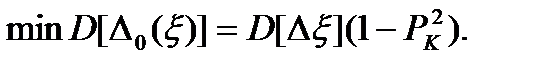(3.47)

Если между составляющими погрешностями АИУ Δξ и Δ_К(ξ) имеется неслучайная связь (чего добиваются компенсацией погрешностей), то Р_К=1 и значение остаточной погрешности может быть равно 0.

Ограничением повышения точности АИУ является невозможность подбора одинаковых параметров влияния основных и дополнительных элементов во всем диапазоне изменения влияющих факторов ξ.