Глава 7 Компенсация веса тела

Конструирование движителей нового типа требует уточнения понятия «открытой и закрытой физической системы», системы отсчета. Повод для размышлений дает тот факт, что вес тела, находящегося на поверхности планеты, зависит от места взвешивания. Поскольку планета вращается, то на все тела действует центробежная сила, и ее максимальное значение соответствует положению тела на экваторе. По данной причине, космодромы для реактивных ракет целесообразно размещать ближе к экватору.

Можно ли получить «отрицательный вес» тела, за счет приложения центробежной силы? Ответ положительный: сила веса может быть компенсирована, и преодолена любой другой силой, в том числе, центробежной силой, создаваемой при вращении тела.

Например, вращение тела в вертикальной плоскости дает полную компенсацию веса в верхней половине траектории, и увеличение веса на величину центробежной силы, в нижней части траектории, рис. 25.

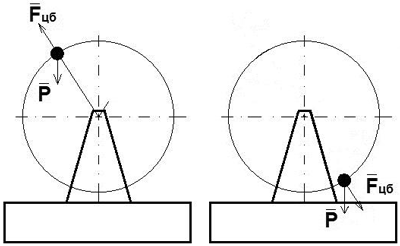
Рис. 25. Изменение веса при вращении тела в вертикальной плоскости

Фактически, вращение груза в вертикальной плоскости, при достижении определенной скорости вращения, способно поднимать весь движитель, отрывая его от земли, во время «верхней половины» цикла. Следовательно, принципиальных проблем нет. Техническая задача состоит в том, чтобы конструктивно обеспечить движение рабочей инерциальной массы по такой траектории, которая дает эффект компенсации веса тела на большей части цикла движения. Например, колебания груза обычного маятника происходят в нижней части цикла, как показано в левой части рис. 26. Процесс колебаний перевернутого маятника показан в правой части рис. 26. Механизм действия «перевернутого маятника» несложный, но его сотни лет изучали как удивительное явление!

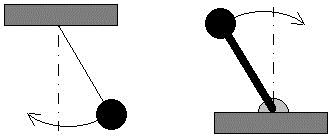
Рис. 26. Обычный маятник и перевернутый маятник

В 1873 году, идея использования перевернутого маятника для строительства летающего аппарата рассматривалась Циолковским, ему тогда было всего 16 лет. Циолковский предлагал использовать для создания движителя два перевернутых маятника, машущих синхронно, во встречных направлениях. Данный эксперимент с парой перевернутых маятников легко организовать, и он показывает наличие импульсных сил. Динамическая стабилизация перевернутого маятника подробно изучалась Академиком П. Л. Капицей в 1951 году [10]. Экспериментальное устройство с кривошипным приводом, построенное для данных экспериментов, рис. 27, получило название «маятник Капицы». Особенностью маятника Капицы является то, что перевернутое (вертикальное) положение маятника может быть устойчивым, в случае быстрых вибраций подвеса.

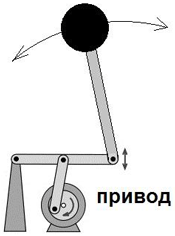
Рис. 27. Маятник Капицы

История открытия уходит в прошлое: первые наблюдения данного явления были опубликованы еще в 1908 г. А. Стефенсоном [11]. Современные исследования аналогичных процессов ведет Профессор Евгений Дмитриевич Сорокодум, автор многих научных статей и интересных экспериментов по вихревым и колебательным процессам [12]. Не будем углубляться в теорию данного процесса, полагая, что основную роль в колебательных процессах перевернутого маятника играют центробежные силы, которые частично компенсируют вес устройства. Мы рассматривали аналогичные явления, показанные на схемах рис. 25 и рис. 16.

Странно, но я не нашел в работах П. Л. Капицы идеи о том, что, повышая частоту колебаний перевернутого маятника, то есть, скорость движения рабочей массы, можно ожидать полной компенсации веса устройства, и даже создание значительной силы тяги, действующей в заданном направлении. Тем не менее, идея простая и работоспособная. Величина силы тяги, в соответствии с законом Ньютона, формула F. 1, зависит не столько от массы, сколько от скорости, так как ускорение пропорционально квадрату линейной скорости. По этой причине, целесообразно работать с малой массой, но на большой скорости, то есть, создавая колебательные процессы высокой частоты.

Существует похожие устройства, которые называют «вибрационные гироскопы». Обычно, они применяются для измерения угловой скорости поворота, при криволинейном движении. Другое применение – создание движущей силы, в настоящее время мало изучено, хотя примеров вибрационных движителей в природе достаточно, чтобы обратить на них внимание. Высокочастотные вибрационные процессы могут быть созданы за счет пьезоэлектрических и других приводов. Пьезоэлектрические системы интересны тем, что они потребляют мало энергии, и могут работать на очень высоких частотах.

Перейдем к другому варианту использования центробежных сил, компенсирующих вес тела. Представим простой эксперимент: мысленно поместите в сферу вращающийся металлический шарик. Допустим, что он приводится в движение не внутренними силами, а внешними полями, например, вращающимся магнитным полем трехфазной системы катушек, расположенной вокруг сферы. Привести во вращение шарик можно и круговыми колебательными движения самой сферы. Вы можете сами провести данный эксперимент, поместив горошину в полусферическую (конусную) чашку. При создании колебательных круговых движений чашки, горошина ускоряется, вращается по внутренней стороне чашки, поднимаясь все выше и выше. Она стремится перейти на орбиту большего радиуса, что вызвано действием центробежной силы. При достаточно большой скорости вращения, горошина вылетает из чашки.

Зададимся целью использовать данный эффект. Напомню старый цирковой трюк: «мотоциклист в шаре». На рис. 28 показаны три траектории мотоциклиста, катающегося по внутренней поверхности сферы. В первом случае, мотоцикл движется по поверхности нижней полусферы, с постепенным увеличением радиуса, а на больших оборотах – вращается по экватору, траектории максимального радиуса.

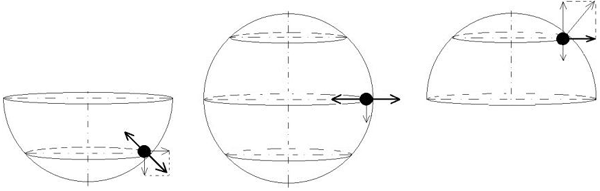
Рис. 28. Движение «рабочего тела» по внутренней поверхности сферы

На рисунке в центре рис. 28, показана траектория движения мотоцикла по экватору сферы. В цирке, при выходе мотоциклиста на траекторию экватора, половинки сферы разъединяли, а нижнюю полусферу опускали, что вызывало искренний восторг публики! Более всего, нас интересует гипотетическая ситуация, показанная в правой части рис. 28. При данной траектории движения «внутреннего рабочего тела», на данное тело должна действовать вертикальная составляющая некой силы, компенсирующей его вес. На корпус устройства (полусферу), в данном случае, будет действовать реактивная сила, направленная вверх.

Представляется возможным создать движитель, использующий данный принцип. При конструировании, необходимо учесть силы трения в точке соприкосновения внутренней поверхности сферы и движущейся рабочей инерциальной массы.

Рассмотрим еще несколько теоретических моделей. На рис. 29 показана схема импульсного движителя, в котором используется два или более вращающихся грузов. Вдоль оси вращения расположен электромагнит, периодически втягивающий сердечник. Поскольку вращающиеся грузы и сердечник связаны гибкой тягой, то движение сердечника вниз происходит с усилием, так как необходимо перевести вращающиеся грузы с орбиты большего радиуса на орбиту меньшего радиуса.

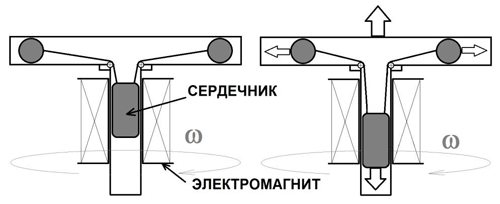
Рис. 29. Импульсный движитель Фролова

Взаимодействие сердечника и катушки электромагнита происходит в соответствии с законом сохранения импульса, поэтому усилие на перемещение сердечника электромагнита передается корпусу, который получает реактивный импульс тяги вверх. Возврат грузов на орбиту большего радиуса происходит без усилий, если электромагнит выключен. Таким образом, данное устройство способно «рывками» подтягиваться вверх. Полагаю, что экспериментальная проверка данной концепции покажет хорошие перспективы внедрения данной технологии в аэрокосмической технике. Еще одна идея использования центробежной силы, сжимающей пружину, показана на рис. 30.

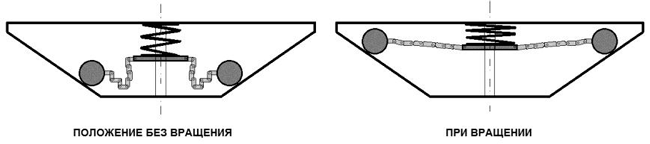
Рис. 30. Пара грузов на плоских цепях

Грузы соединены с осью вращения плоскими цепями, не передающими осевое усилие. Без вращения, грузы лежат на дне корпуса, а пружина расслаблена. При вращении оси, например, электроприводом, грузы приходят в движение, поскольку плоские цепи передают крутящий момент. При определенной скорости вращения, грузы выходят на орбиту наибольшего радиуса, натягивая плоскую цепь, которая их соединяет. Натяжение цепи приводит к сжатию пружины, которая упирается в корпус. Теоретически, предполагается, что корпус получит импульс, в процессе сжатия пружины. После ее сжатия, на корпус оказывается только постоянное давление. Упругое сжатие пружины обеспечивается центробежными силами. Аналогично предыдущему варианту конструкции, можно организовать импульсный режим работы, например, за счет периодического изменения скорости вращения грузов, или другим способом. Грузов в схеме, показанной на рис. 30, может быть несколько.

Можно предложить еще много теоретических моделей, основанных на похожих принципах, но теория без практики не имеет коммерческого смысла. Предлагаемые конструкции несложные, дешевые по себестоимости для любой мощности привода, интересно было бы их проверить экспериментально.

Перейдем к примерам известных реальных движителей, уже проверенных на практике, в которых используются инерциальные эффекты.

Глава 8 Инерциоиды

Мы уже начали рассматривать конструкции механических устройств, движущая сила в которых обусловлена применением свойства инерциальности частиц материи, то есть, их связи с эфиром. Данный тип движителей называется «инерциоиды», термин придумал инженер В.Н. Толчин, в 1936 году [13]. На фотографии рис. 31 показан один из инерциоидов Толчина. Принцип действия очень простой: два грузика вращаются синхронно, в разных направлениях, что компенсирует крутящий момент.

Рис. 31. Инерциоид Толчина

Каждый из них, на половине траектории, разгоняется приводом, а на второй половине траектории привод выключается, а включается тормозная колодка (пружинный тормоз), вращение тормозится. Такой режим «мотор – тормоз» позволяет передавать реакцию корпусу устройства во время всего цикла, как при ускорении инерциальных масс, так и при их торможении.

На схеме рис. 32 показаны две фазы работы подобного движителя: разгон эксцентриков приводом, а затем, их свободное движение, которое тормозится.

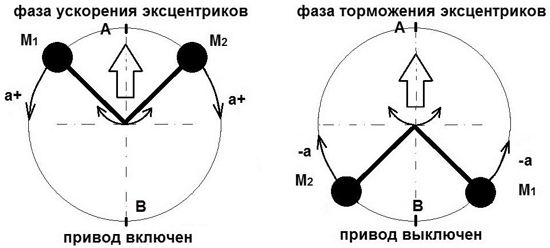
Рис. 32. Две фазы работы инерциоида

При разгоне, от точки А до точки В, ускорение положительное, и при свободном движении, от точки В до точки А, ускорение отрицательное (торможение). Реакция корпуса на обе половины цикла направлена в одну сторону, хотя ее величина меняется, в связи с чем, устройство двигается рывками. Отметим, что в инерциоиде Толчина углы включения мотора или тормоза были равны 30 градусов: от 330 до 0 градусов работал мотор, а от 150 до 180 градусов происходило торможение. В общем случае, фазы ускорения и торможения могут составлять по половине цикла.

В своих работах, А.Е. Акимов и Г.И. Шипов, раскрывают теорию работы инерциоидов с позиций «торсионной механики». Г.И. Шипов приложил много усилий для практического развития данной темы, еще в 1981 году изготовил два инерциоида по схеме Толчина в фирме Туполева, а затем успешно испытал их в МГУ, устанавливая инерциоид для испытаний на «платформу на воздушной подушке» [14].

Интересно, что при попытке Шипова подать заявку на изобретение в 1991 году, он получил отказ, обоснованный тем, что существует некое Постановление, запрещающее российскому патентному бюро принимать к рассмотрению заявки по данной теме. Формулировка «движение системы за счет внутренних сил» может быть изменена только в том случае, если Академия Наук официально признает существование эфира, как реальной среды, имеющей определенные физические свойства.

Тем не менее, экспериментально, эффект Толчина и работоспособность его инерциоида были подтверждены неоднократно, еще в тем времена, когда Шипов работал с Ракетно‑Космической Корпорацией «Энергия», а также, в ходе совместных экспериментов с американскими учеными. В 2000 году, Шипов изучал тему инерциоидов в лаборатории, которую специально создали в Таиланде. Наконец, в 2002 году, НИИ Космических систем имени Хруничева начал серьезно заниматься темой инерциальных движителей, о чем говорит факт применения новой системы корректировки орбиты спутника «Юбилейный».

История инерциоидов, судя по старым патентным документам, показывает наличие большого интереса изобретателей к данной теме. Очевидно, что есть спрос на подобную технику. Отчасти, это объясняется тем, что данные устройства довольно примитивны, не требуют электроники, и могли быть успешно реализованы много лет назад. В статье «Свободная энергия», 1996 год, я привел ссылки на десятки патентов по теме «инерциоиды» [15]. В 2003 году, в журнале «Новая энергетика» был дан обзор конструктивных решений инерциоидов, по схемам американских патентов [16]. Более ста схем инерциоидов рассмотрено на популярном интернет сайте www.rexresearch.com/inertial/inertial.htm

Публике мало известно о масштабах работ правительственных лабораторий в данном направлении, полагаю, что их данные засекречены. В открытых средствах массовой информации можно найти публикации о проектах частных исследовательских фирм и изобретателей. Одним из ярких исторических примеров в данной области является «инерциоид Дина».

Страховой агент из Вашингтона, Норман Л. Дин (Norman L. Dean) получил американский патент № 2,886,976 13 июля 1956 года. Устройство называется "System For Converting Rotary Motion Into Unidirectional Motion”, то есть, «система преобразования вращательного движения в однонаправленное». Второй патент взят позже, US Patent № 3,182,517 от 11 мая 1965 года «Variable Oscillator System», название означает «Система с изменяемым осциллятором».

Критики работ Нормана Дина выражают свои сомнения по поводу его результатов, так как собрав аналог его изобретения строго по описанию, взятому из патента, они не получают работоспособного движителя. Предполагается, что автор описал в тексте патента принцип в сокращенном виде, не раскрывая некоторые важные детали конструкции.

На рис. 31 показан автор данного изобретения Норман Дин, и его движитель. Это не один инерциоид, а несколько парных инерциоидов, каждый из них имеет по два встречных вращающихся эксцентрика, что позволяет устройству в целом хорошо компенсировать вибрации.

Рис. 33. Норман Дин и его движитель

На рис. 34 показан рисунок из патента № 2,886,976, к которому добавлены названия основных деталей конструкции «движителя Дина».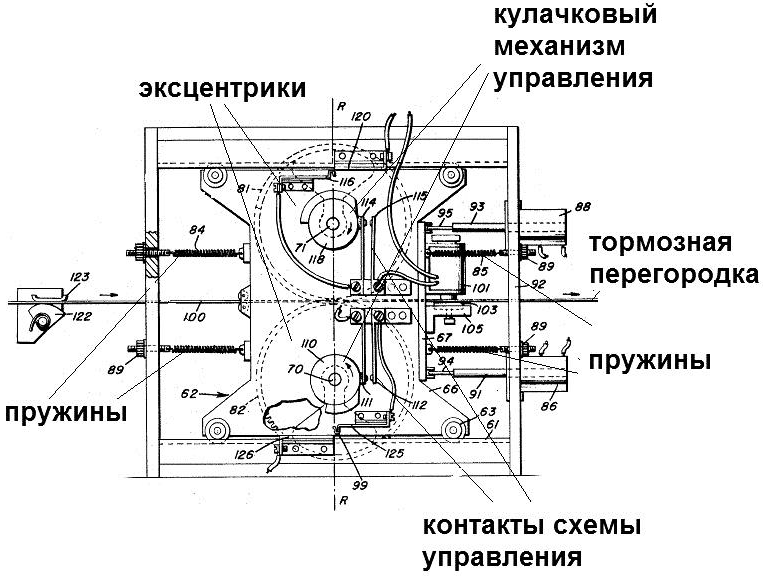

Рис. 34. Схема движителя Нормана Дина

Особенность конструкции «машины Дина» в том, что эксцентрики подвешены в корпусе упруго, на пружинах. Первоначально, Дин просто экспериментировал с парой эксцентриков, закрепленных на перемычке, которая, с помощью пружин, крепится к корпусу аппарата, как показано на рис. 35.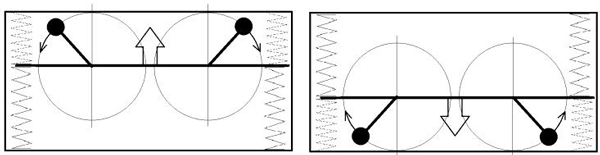

Рис. 35. Компенсация боковых колебаний двумя эксцентриками

Перемычка и эксцентрики – это пара взаимодействующих тел. Их взаимодействие происходит в соответствии с законом сохранения импульса. Цикл движения эксцентриков делится на два полуцикла, создавая компенсацию силы тяжести на половине цикла. Рассмотрим цикл вращения, рис. 35: движение эксцентриков вниз вызывает реакцию опоры, начинается движение перемычки вверх. Далее, движение эксцентриков вверх вызывает реакцию опоры, которая проявляется как движение перемычки вниз. Поскольку вращение двух эксцентриков (пары) встречное, то Дину удалось компенсировать боковые колебания корпуса, а перемычка с вращающимися эксцентриками колебалась по вертикали. Как и следовало ожидать, суммарный импульс силы, действующий на корпус данного устройства за длительный интервал времени, был равен нулю.

Далее, Дин создал «асимметрию цикла», которую мы обсуждали в схеме Толчина. В нужный момент, в конструкции включается «тормоз», рис. 36. В момент прохождения перемычки через среднее положение, она упирается в выдвижной поперечный тормоз, управляемый электромагнитом. В результате, получаются разные по величине силы взаимодействия колеблющейся вверх‑вниз перемычки с корпусом.

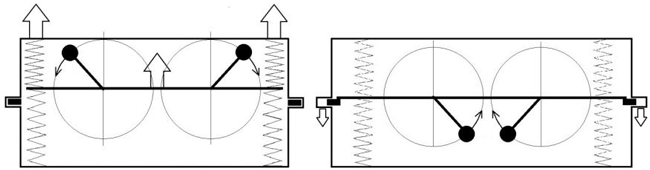
Рис. 36. Идея движителя Нормана Дина

Выбрав правильный момент торможения, можно получить однонаправленную суммарную силу, в нужном направлении. Движитель с одной парой эксцентриков работает рывками, поэтому Дин соединил шесть движителей вместе, но расположение эксцентриситета на каждом из них сдвинул на угол 60 градусов. Таким образом, он получил полный цикл 360 градусов, и более‑менее равномерную однонаправленную силу тяги. Анализируя процесс энергообмена в движителе Дина, необходимо отметить важную роль упругого взаимодействия, хотя этот аспект мало обсуждается в публикациях по данной теме. В устройстве Дина, происходит упругая передача импульса от перемычки корпусу в одну сторону (вверх), и неупругое торможение перемычки о поперечный тормоз, при движении в другую сторону. Теоретически, данная задача хорошо проработана, и относится к физике взаимодействия тел.

Известно, что столкновение тел может приводить к разным результатам: при упругом столкновении тела и корпуса устройства, в основном, корпусу передается импульс, а при неупругом столкновении (ударной деформации) большая часть импульса преобразуется в тепло. Схема эксперимента, который был мной показан аудитории конференции «Новые Идеи в Естествознании», в 1996 году, изображена на рис. 37.

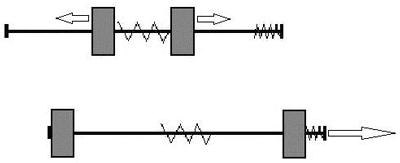
Рис. 37. Эксперимент по упругому и неупругому взаимодействию

Идея эксперимента довольно старая, она была опубликована, хотя и без объяснений причин данного явления, еще в 1935 году [17]. Итак, предположим, что на направляющем стержне могут скользить влево и вправо два грузика с отверстиями, например, два свинцовых цилиндра диаметром 15 мм и высотой 30 мм. Между ними расположена пружина, которая в начальный момент сжата, и удерживается в данном положении нитью. В правой части оси, был установлен резиновый амортизатор толщиной 5 мм.

На рис. 38 показаны три последовательных кадра из видеозаписи данного эксперимента, который проводился на полированном столе в аудитории конференции «Новые идеи в естествознании», 1996 год. Суть эксперимента состоит в следующем: нить, которая удерживает пружину в сжатом состоянии, разрушают каким‑либо образом, например, пережигают. Тела, оттолкнувшись друг от друга в центральной точке корпуса, скользят в разные стороны, и каждое из них, по‑разному, взаимодействует с опорой в конце своего пути.

Рис. 38. Эксперимент по асимметрии взаимодействия

С той стороны, где взаимодействие упругое (справа установлен амортизатор), опоре передается больший импульс, в результате чего, она сдвигается в данную сторону. С другой стороны (слева) тело ударяется об опору жестко, большая часть его кинетической энергии преобразуется в тепловые деформации. Положение устройства на столе, до и после взаимодействия тел с корпусом, отличается: после взаимодействия, устройство сдвигается в ту сторону, где установлен амортизатор. Данный опыт легко повторим, в том числе, на подвесе, на плавающей платформе и т. п. В каждом случае, суммарный импульс, передаваемый корпусу данного устройства в результате взаимодействия, не равен нулю, следовательно, в аналогичной конструкции движителя, мы можем получать однонаправленный импульс периодически, причем, без видимого взаимодействия с внешней средой, то есть, с какой либо опорой. Тем не менее, взаимодействие с окружающей средой здесь также есть, поскольку этот эксперимент – один из вариантов асимметричного «энтропийного движителя», описанного ранее, и показанного на рис. 1. С одной стороны, в данном экспериментальном устройстве энтропия минимальная, здесь создается макроимпульс, передаваемый корпусу движителя через амортизаторы, как и в движителе Дина. С другой стороны, энтропия процесса взаимодействия намного больше, так как частицы вещества получают при взаимодействии, в основном, неупорядоченные импульсы, а в результате деформаций, выделяется тепловая энергия, которая передается окружающей среде.

Итак, движение может быть создано в результате асимметричного (в пространстве) энергообмена с окружающей средой. Позже, в главе о нанотехнологиях, мы вернемся к этому вопросу, показав еще один метод реализация данного принципа. Сейчас вернемся к механическим системам, использующим инерциальные свойства тела, движущегося по траектории переменного радиуса кривизны.

Эффективность таких инерциоидов может быть очень высокая, например, в 1980‑е годы в Канаде и США испытывали инерционный привод по схеме Торнсона (Brandson R. Thomson), в котором эксцентрики двигаются по траектории кардиоиды. Данный привод был достаточно мощный для того, чтобы обеспечивать движение лодки с пассажирами. По энергозатратам, данный привод экономнее, чем бензиновый лодочный винтовой мотор примерно в 20 раз. Изобретение подробно описано в патенте US 4631971, от 30 декабря 1986 года.

Рассмотрим схему инерциоида Торнсона, рис. 39. Серыми кружками на схеме показано положение эксцентрика при его движении, которое создается путем суммирования двух движений: орбитального и собственного вращения. Применение пары эксцентриков позволяет устранить боковой импульс, передаваемый корпусу.

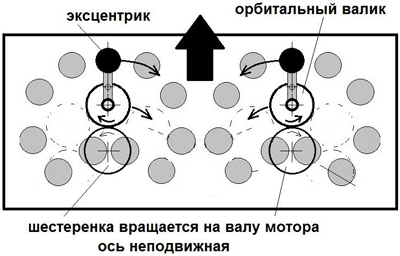
Рис. 39. Схема инерциоида Торнсона

Орбитальный валик «обкатывает» шестеренку, которая установлена на валу мотора. Моторов может быть два, но они должны работать синхронно. Обычно, для каждого эксцентрика создают свою шестеренку привода, которую «обкатывает» орбитальный валик, но оба привода синхронизированы, поскольку имеют один общий мотор. Экспериментальные данные, подтверждающие перспективность схемы Торнсона, были получены моим братом Фроловым Алексеем Владимировичем. При наличии интереса заказчиков к данной теме, мы готовы разработать комплект конструкторской документации для изготовления привода по схеме Торнсона.

В настоящее время, разработаны компьютерные программы для моделирования кардиоиды и конструирования инерциоидов Торнсона. На рис. 40 показан один из вариантов конструкторского решения, в котором две подвижных шестеренки обкатывают неподвижную центральную шестеренку.

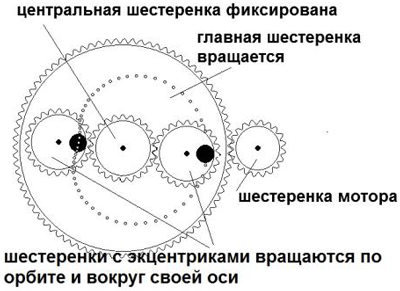
Рис. 40. Компьютерное моделирование инерциоида

Итак, если траектория движения центра масс имеет форму кардиоиды, то центробежная сила, и сила реакция на корпус устройства, имеет разную величину в разных направлениях. Движущая сила обусловлена здесь, как и в других похожих схемах, градиентом центробежной силы. В настоящее время, авторов изобретений по теме «инерциоиды» очень много. Хотелось бы рассказать про тех, кого я знал лично. Примером многолетней бескорыстной исследовательской работы в данном направлении являются проекты Константина Дмитриевича Шукалова, Иваново. В 1996 году, он приезжал в Санкт‑Петербург на конференцию, и демонстрировал свои модели в работе, рис. 41.

Рис. 41. Константин Дмитриевич Шукалов демонстрирует один из своих инерциоидов, 1996 год

Одна из моделей Шукалова показана на рис. 42. В данной конструкции привода, питание на электромагнит подается по проводу. Два эксцентрика движутся по траектории постоянного радиуса, но их взаимодействие имеет особенность: в одном крайнем положении, они ударяются друг о друга, импульс «гасится». В другом крайнем положении, они ударяются о пружины, передавая корпусу два сонаправленных импульса.

Рис. 42. Один из инерциоидов Шукалова

По поводу закона сохранения импульса, для рассматриваемой конструкции, необходимо отметить, что при соударении грузов, их импульс преобразуется в тепловую энергию деформации вещества, из которого сделаны движущиеся грузы. При сжатии пружин, в другой фазе рабочего цикла, энергия частично преобразуется в тепло, но большая часть кинетической энергии движущихся грузов передается корпусу движителя. Данная схема Шукалова представляется весьма перспективной для практического внедрения.

Практическое применение таких приводов возможно не только в авиации, на судах или в космосе, но и в роли привода любой колесной техники, причем технологически устраняется система передачи крутящего момента на колеса (трансмиссия) и создается качественно новый уровень техники. Все, что требуется для внедрения данной перспективной технологии на транспорте, это интерес заказчиков и инвесторов.