Фильтрация погрешностей
Эффективным способом снижения действия помех, а, следовательно, и погрешностей, в АИУ является фильтрация. Особенно эффективно действие фильтрации, когда спектры полезного сигнала АИУ и помехи не перекрываются. Однако и в случае пересечения спектров информационного сигнала и помехи фильтрация позволяет значительно уменьшить действие помех на работу прибора. В аналоговой СИ чаще применяется линейная фильтрация, а при расчете СИ исходят из того, что результат фильтрации не может быть идеальным. В СИ всегда остается погрешность от действия помех, однако, она становится минимальной при правильном выборе фильтра или его параметров.
Выбор оптимальных параметров фильтра.Пусть в СИ действует аддитивная смесь полезного сигнала и помехи со спектральными плотностями 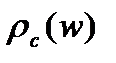 и
и 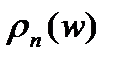 . Сигнал и помеха стационарны и некорректированы. Полезный сигнал менее широкополосен, чем помеха, и его спектральная плотность падает с ростом частоты. В этом случае существует некоторое оптимальное значение полосы пропускания фильтра нижних частот
. Сигнал и помеха стационарны и некорректированы. Полезный сигнал менее широкополосен, чем помеха, и его спектральная плотность падает с ростом частоты. В этом случае существует некоторое оптимальное значение полосы пропускания фильтра нижних частот 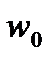 , минимизирующее значение СКО погрешности от действия помех в СИ. Определим
, минимизирующее значение СКО погрешности от действия помех в СИ. Определим 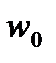 . Для этого найдем СКО погрешности от искажения измерительного сигнала при прохождении его через фильтр
. Для этого найдем СКО погрешности от искажения измерительного сигнала при прохождении его через фильтр 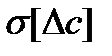 и погрешности из-за прохождения части помех через этот фильтр
и погрешности из-за прохождения части помех через этот фильтр 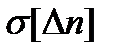 :
:
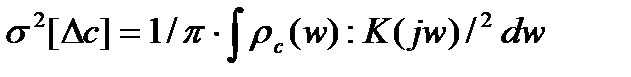 , (3.85)
, (3.85)
где K(jw) – частотная характеристика фильтра или самого СИ:
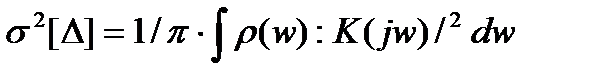 . (3.86)
. (3.86)
Суммарную погрешность фильтрации определяем из соотношения:
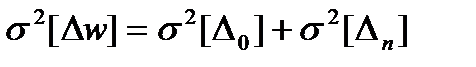 . (3.87)
. (3.87)
Можно найти значение 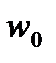 , минимизирующее суммарную погрешность фильтрации, решив уравнение вида:
, минимизирующее суммарную погрешность фильтрации, решив уравнение вида:
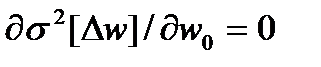 . (3.88)
. (3.88)
Если частотная характеристика СИ или ФНЧ близка по виду к частотной характеристике идеального фильтра, то решение упрощается. В таком случае:
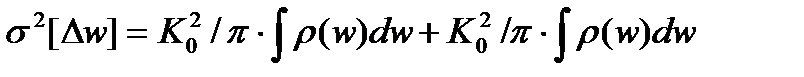 , (3.89)
, (3.89)
где К0 – номинальный передаточный коэффициент СИ.
Рассмотрим пример: пусть 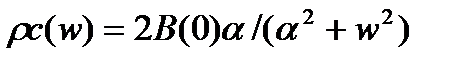 ;
; 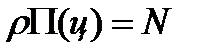 . Тогда
. Тогда
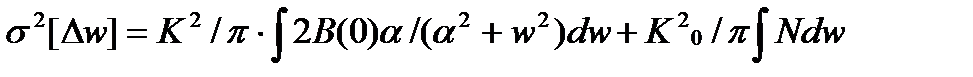 .
.
Откуда 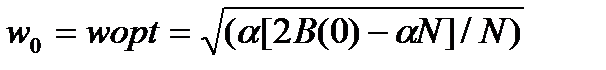
Оптимальная линейная фильтрация.Будем полагать, что на входе СИ действуют такие же сигналы, что и в случае, рассмотренном ранее. Известно, что фильтр (или СИ) для неискажающей передачи формы сигнала должен иметь линейную фазочастотную характеристику 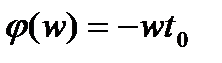 .
.
Тогда спектральная плотность помехи, прошедшей через искомый фильтр, будет иметь вид:
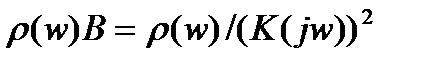 , (3.90)
, (3.90)
где K(jw) – комплексная частотная характеристика искомого фильтра. Измеренный сигнал подвергается линейному преобразованию L , а сигнал погрешности после такого преобразования имеет вид:
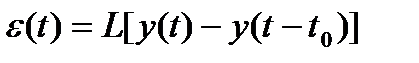 . (3.91)
. (3.91)
Преобразование Фурье этого сигнала:
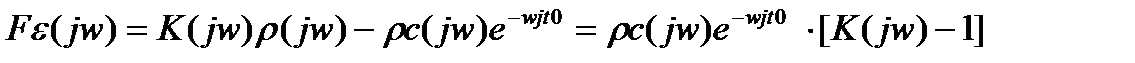 , (3.92)
, (3.92)
а энергетический спектр погрешности:
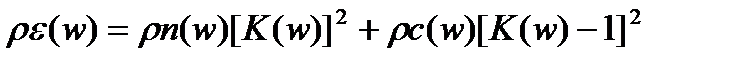 . (3.93)
. (3.93)
Найдем минимальное значение 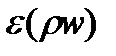 из выражения:
из выражения:
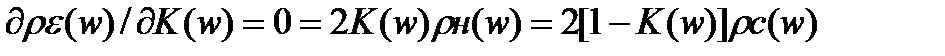 . (3.94)
. (3.94)
Откуда
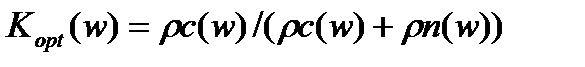 , (3.95)
, (3.95)
а физически реализуемый оптимальный фильтр имеет передаточную характеристику:
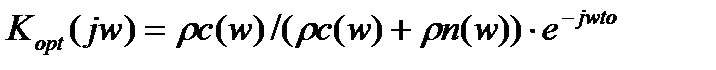 (3.96)
(3.96)
Подставив в выражение (94) значение 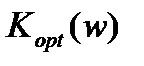 , получим формулу для определения минимального значения погрешности фильтрации:
, получим формулу для определения минимального значения погрешности фильтрации:
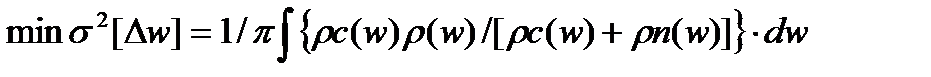 . (3.97)
. (3.97)
Дата добавления: 2015-12-29; просмотров: 1005;
