Стабилизация реальной характеристики преобразования

способом стабилизации реальной характеристики преобразования , широко применяемым на практике, является способ отрицательной обратной связи (ООС) (рисунок 3.5).

Рис.3.5. Способ отрицательной обратной связи (ООС)

Здесь ПП, ОП – прямой и обратный преобразователи. Этот способ является универсальным, т.к. с помощью ОС уменьшается суммарный эффект от действия разнообразных дестабилизирующих факторов. ОС почти всегда применяется в точных СИ, однако, с помощью только одной СИ невозможно решить задачу повышения точности во всех случаях их работы. В статистическом режиме работы СИ в ОС предельное значение аддитивной погрешности, приведенной к выходу 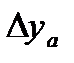можно определить из соотношения:

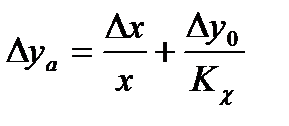, (3.32)

где 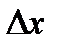и 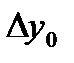– предельное значение аддитивной погрешности прямой и обратной цепе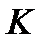й;

и 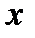– передаточные коэффициенты прямой ПП и обратной ОП цепей.

Из выражения (3.32) видно, что если аддитивная погрешность действует на входе устройства, то при 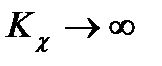она полностью устраняется. Если же аддитивная погрешность действует на выходе , то она не устраняется введением ОС. В этом случае относительная аддитивная погрешность равна:

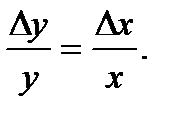(3.33)

Предельное значение относительной мультипликативной погрешности при ООС можно найти из соотношения:

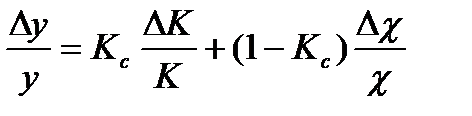, (3.34)

где 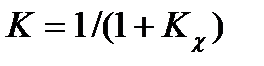– коэффициент статизма ; 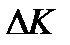и 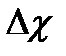– абсолютные мультипликативные погрешности прямой и обратной цепей.

при 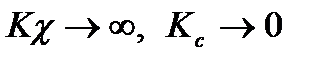суммарной погрешности равно погрешности цепи ООС. При этом предполагается, что осуществляется статическое регулирование относительно влияющих факторов, приложенных к входу устройства. На практике для получения малого влияния нестабильности прямой цепи АИУ на его работу, необходимо сделать значение 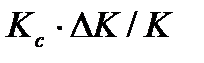в 3 – 5 раз меньше значения 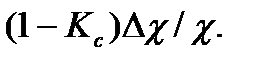Дальнейшее уменьшение статизма нецелесообразно и приводит лишь к незначительному уменьшению мультипликативной погрешности и может возникнуть необходимость введения сложных цепей стабилизации работы прибора.

Комплексную передаточную характеристику 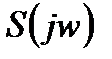с цепью ОС можно записать в виде:

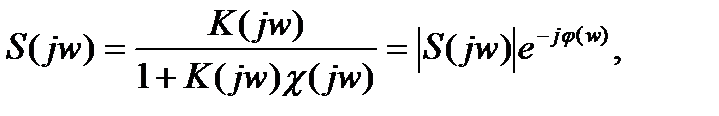(3.35)

где 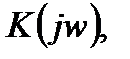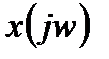– комплексная характеристика преобразования прямой и обратной цепей.

Если обозначить через φ_K =φ_K(w) и φ_χ =φ_χ(w) – соответственно сдвиги фаз, вносимые прямой и обратной цепями, а 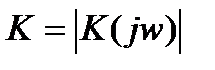и 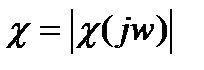, то можно записать:

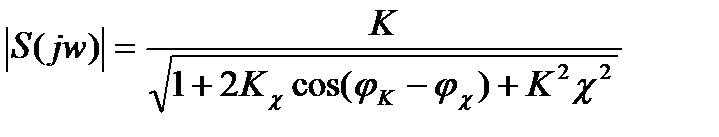(3.36)

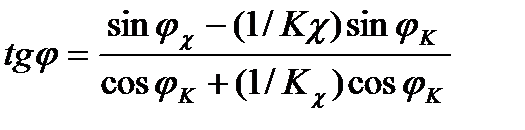
При К_χ >> 1 получим:

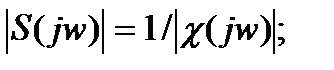
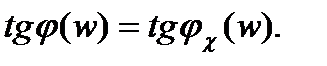(3.37)

Из выражения (3.36) видно, что нестабильность коэффициента передачи уменьшиться в 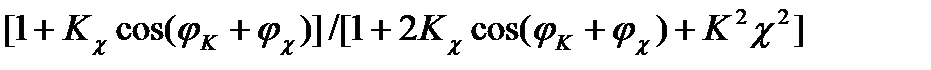раз, а влияние фазового сдвиги прямой цепи в раз. Если предположить, что погрешности случайные величины, то на основании (3.32), (3.34) можно записать значение дисперсии относительной аддитивной σ_a² и мультипликативной σ_M² погрешностей с ООС:

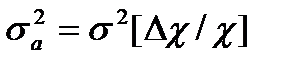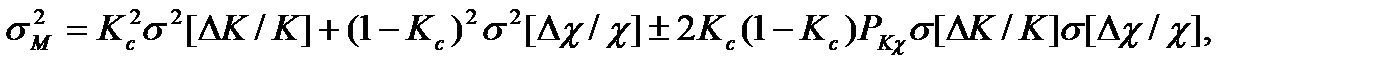, (3.38)

где 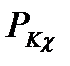– коэффициент корреляции погрешностей прямой и обратной цепей.

Минимальное значение погрешности при К_с << 1 и при условии нулевого порога чувствительности преобразователя прямого канала равно погрешности цепи ОС:

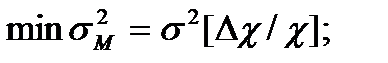
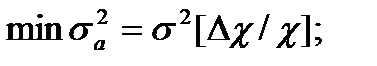(3.39)

При конечном пороге чувствительности появляется погрешность:

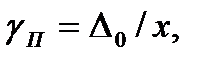(3.40)

где 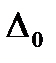– порог чувствительности прямой цепи; х – значение входного сигнала.

Способ отрицательной обратной связи, при условии линейности преобразователя ОС, позволяет уменьшить погрешность нелинейности

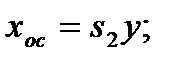
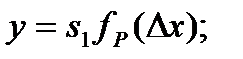
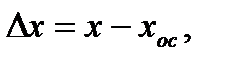(3.41)

где 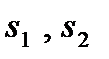– чувствительность прямой и обратной цепей, f_P – передаточная характеристика прямой цепи. Решив эти уравнения относительно y, получим:

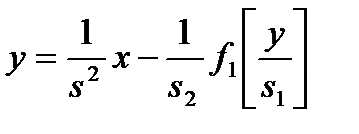. (3.42)

при 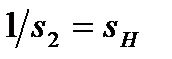, где s_H – номинальная чувствительность, и 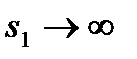имеем идеальную характеристику преобразования:

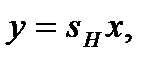(3.43)

недостатки при реализации способа ООС:

1. Необходима избыточность прямой цепи по чувствительности.

2. ограниченность возможности уменьшения погрешностей, так как при больших значениях усиления замкнутой цепи 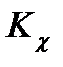теряется устойчивость.

3. При больших значениях усиления замкнутой цепи 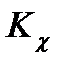может наблюдаться подъём АЧХ АИУ в рабочей области частот, то есть требования к точности и широкополосности АИУ противоречивы.

4. Введение ОС увеличивает полосу пропускания селективных АИУ.