Число степеней свободы

Представим себе стержень АВ на неподвижной оси вращения О. Чтобы однозначно определить положение всех точек, очевидно, достаточно задать закон изменения угла поворота стержня.

Возьмем кривошипный механизм. Здесь тоже положение всех точек определяется заданием одного угла поворота кривошипа. Теперь представим центробежный регулятор, вращающийся вокруг вертикальной оси. Для того чтобы вполне определить положение любой точки, необходимо задать две величины – угол j и угол a. Или, например, рассмотрим материальную точку, находящуюся на плоскости. Для задания ее положения в двух взаимно перпендикулярных направлениях необходимо задать координаты x и y. Эти системы обладают двумя степенями свободы.

Вообще, если положение всех точек системы вполне определяется заданием К независимых величин, то говорят, что система имеет К степеней свободы.

Число независимых между собой возможных перемещений механической системы называется числом степеней свободы этой системы.

У свободной точки три степени свободы – вдоль координат х, у, z. У свободного твердого тела – 6 степеней свободы: три линейных перемещения вдоль осей х, у, z и три поворота относительно этих трех осей.

Идеальные связи

Представим механическую систему, состоящую из материальных точек 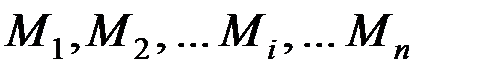. Пусть каждая точка этой системы подчинена двусторонней связи. Реакции связей обозначим через R₁, R₂, ... R_n . Сообщим системе какое-либо возможное перемещение. Перемещения точек системы обозначим через .

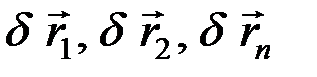Вычислим сумму работ реакций связей на этих перемещениях. Если сумма работ равна нулю для всех возможных перемещений системы, то данная связь называется идеальной.

Идеальными называются связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю:

.

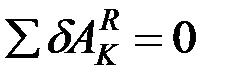Докажем, что если механическая система с идеальными связями находится в равновесии под действием приложенных сил, то при любом возможном перемещении системы должно выполняться равенство:

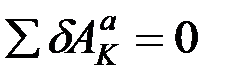
или

,

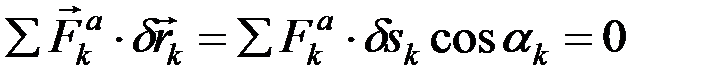где a – угол между силой и возможным перемещением.

Обозначим силы, действующие на точку через 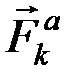и 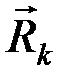, тогда для каждой точки системы 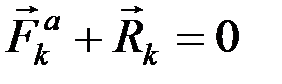, т.к. система находится в равновесии, а следовательно, и сумма работ этих сил при любом перемещении точки равна нулю:

.

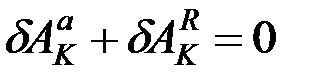Составив такие равенства для всех точек системы и сложив их почленно, получим

.

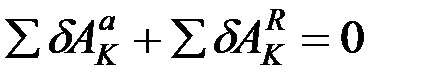Так как связи идеальные, второе слагаемое равно нулю, тогда равна нулю и первая сумма.