Лекция 15 УРАВНЕНИЯ ЛАГРАНЖА II-ГО РОДА
Обобщенные координаты системы. Обобщенные силы
и способ их вычисления. Уравнения Лагранжа II-го рода
Обобщенными координатами механической системы называются величины, заданием которых вполне определяется положение всех точек системы.
Числом степеней свободы системы называется число независимых обобщенных координат, определяющих положение точек системы.
Рассмотрим механическую систему, состоящую из п материальных точек М1, М2, … Мп, имеющую К степеней свободы. Обозначим ее независимые обобщенные координаты q1, q2, … qk. Они вполне определяют положение всех точек системы. Тогда декартовы координаты системы будут функциями обобщенных координат:
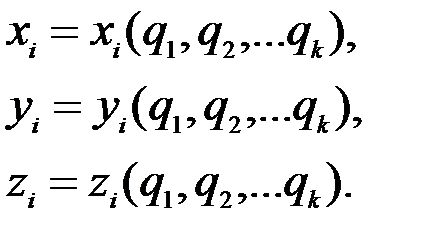
Эти соотношения имеют место только в том случае, когда связи не зависят от времени. Возможно существование связей, изменяющихся с течением времени.
Пример: нить маятника тянут за конец А с постоянной скоростью V.
Пусть ОМ = l , тогда 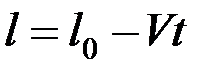 ,
,
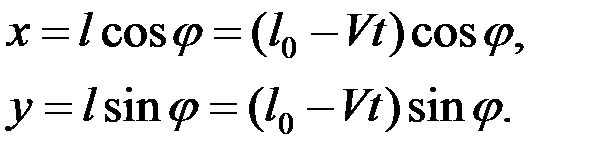
Очевидно, что в данной задаче декартовы координаты – не только функции обобщенной координаты j, но и времени t.
В этом случае имеем:

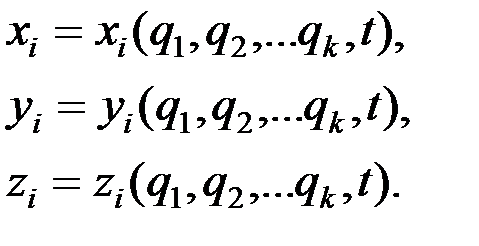
Связи, не зависящие от времени, называются склерономными (или стационарными), а изменяемые с течением времени – реономными (или нестационарными).
Обобщенные силы
Рассмотрим механическую систему, состоящую из п материальных точек: М1, М2, … Мп, имеющую К степеней свободы. Обозначим ее независимые обобщенные координаты q1, q2, … qk. Предположим, что к точкам системы приложены силы 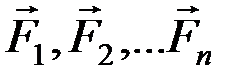 . Чтобы вычислить обобщенную силу, дадим координате q1 ничтожно малое приращение dq1 , оставляя прочие координаты без изменения. Это изменение координаты q1 вызовет ничтожно малые перемещения e1, e2, eп всех точек системы. Вычислим сумму работ сил
. Чтобы вычислить обобщенную силу, дадим координате q1 ничтожно малое приращение dq1 , оставляя прочие координаты без изменения. Это изменение координаты q1 вызовет ничтожно малые перемещения e1, e2, eп всех точек системы. Вычислим сумму работ сил 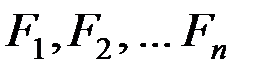 на перемещениях e1, e2, eп:
на перемещениях e1, e2, eп:
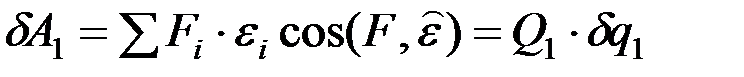 .
.
Пусть эта работа равна произведению некоторого множителя Q1на приращение координаты dq1. Поступая аналогично, найдем Q2, … Qk, соответствующие координатам q2, … qk:
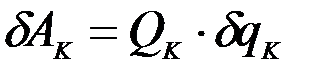 .
.
Обобщенная сила – это величина, равная коэффициенту при приращении обобщенной координаты в выражении полной элементарной работы действующих на систему сил.
Не следует считать, что обобщенная сила всегда имеет размерность [Ньютон]. Работа всегда вычисляется в джоулях (1 Дж =1 Н×м).
| Размерность обобщенной координаты | Размерность обобщенной силы |
| м | Н |
| рад | Н×м |
| м3 | Па |
В механической системе с идеальными связями обобщенные реакции связей всегда равны нулю, поэтому при переходе к обобщенным силам реакции связей автоматически выпадают из расчетов. В этом большое преимущество методов Лагранжа.
Дата добавления: 2015-12-26; просмотров: 653;
