Условие равновесия системы в обобщенных силах
Согласно принципу возможных перемещений, необходимым и достаточным условием является равенство нулю суммы элементарных работ всех активных сил на любом возможном перемещении системы 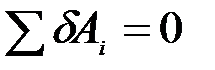 , тогда
, тогда
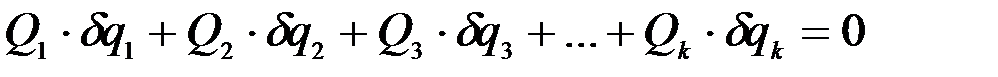 .
.
Так как обобщенные координаты 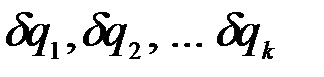 не зависят друг от друга, то равенство выполнимо только в том случае, если каждое слагаемое равно нулю, т.е.
не зависят друг от друга, то равенство выполнимо только в том случае, если каждое слагаемое равно нулю, т.е. 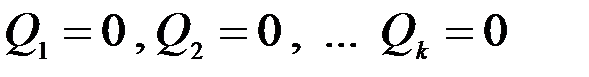 .
.
Для равновесия механической системы необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным для системы обобщенным координатам, были равны нулю.
Уравнения Лагранжа
Для определения уравнений движения в обобщенных координатах обратимся к общему уравнению динамики:
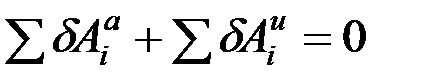 .
.
Пусть система имеет k степеней свободы. Тогда
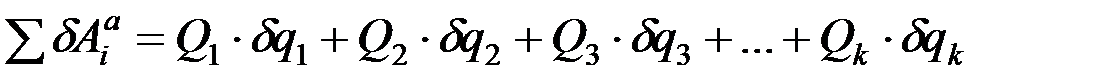 ,
,
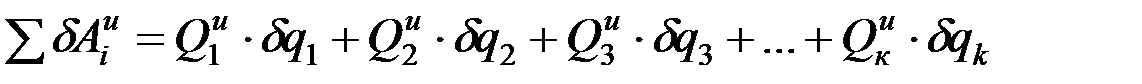 .
.
Подставляя в общее уравнение динамики, получим:
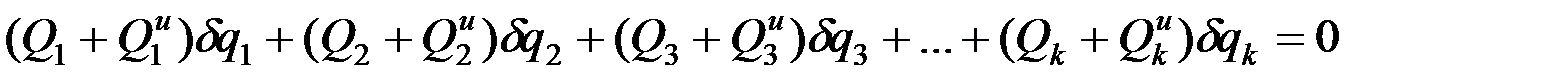
или
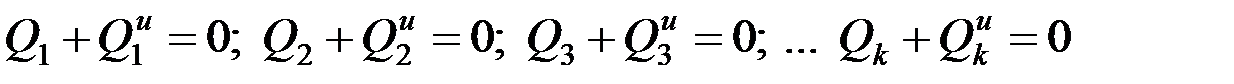 ,
,
где 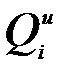 – обобщенные силы инерции, которые равны
– обобщенные силы инерции, которые равны
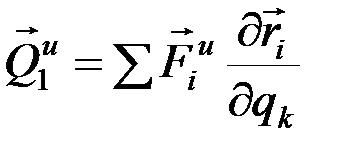 .
.
Так как 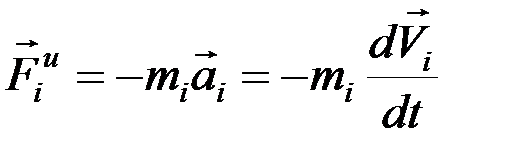 , то
, то
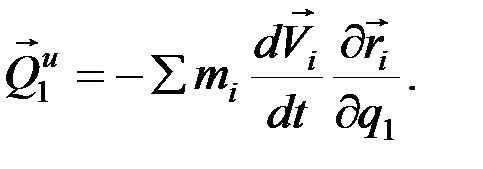 (1)
(1)
Выразим обобщенную силу через кинетическую энергию. Имеем
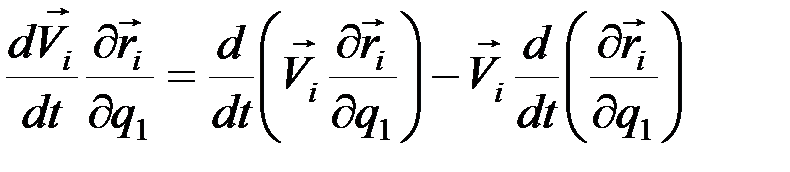 , (2)
, (2)
так как 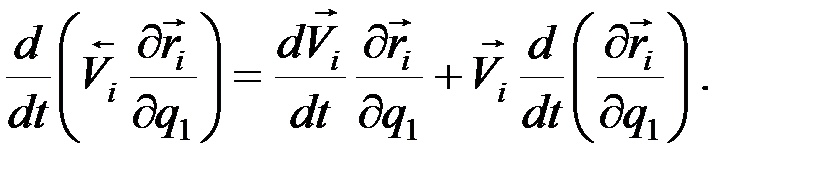
Заметим, что
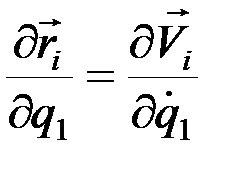 ,
,
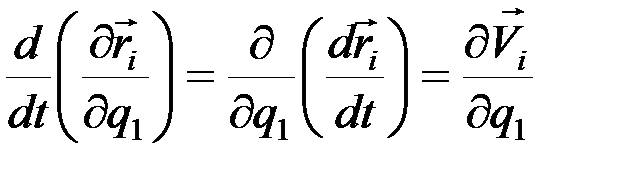 .
.
Подставим полученные выражения в уравнение (2):
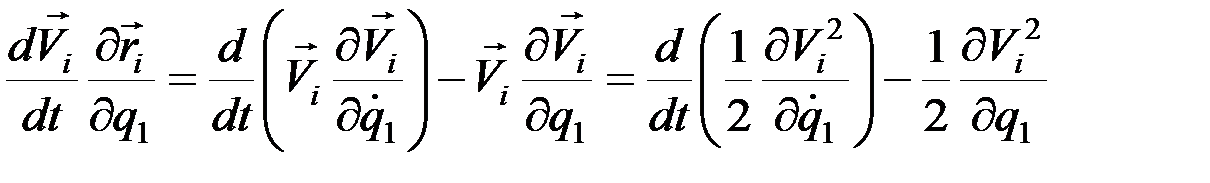 .
.
Тогда уравнение (1) примет вид:
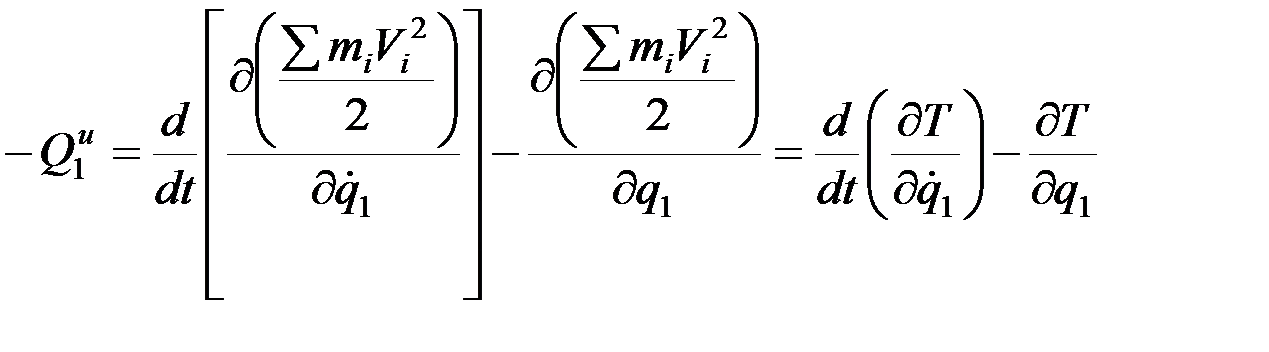 ,
,
где Т – кинетическая энергия.
Аналогичные выражения получаем для всех остальных обобщенных координат. Поскольку 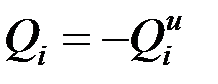 , то
, то
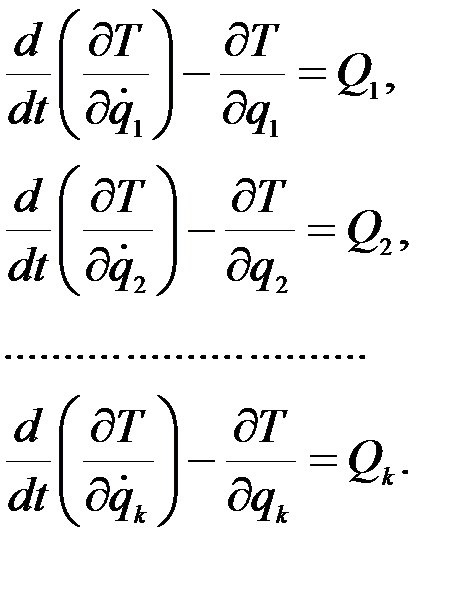
Это дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа II-го рода (уравнения в частных производных). Число этих уравнений равно числу степеней свободы системы.
Основные преимущества использования уравнений Лагранжа при решении задач:
1) количество уравнений не зависит от количества тел, входящих в систему;
2) данный способ позволяет исключить из рассмотрения все неизвестные реакции связей.
Пример.Механизм робота-манипулятора состоит из колонны для вертикального перемещения, устройства для горизонтального перемещения, состоящего из звеньев 1 и 2, и выдвигающейся горизонтальной руки со схватом 3. Массы звеньев механизма т1, т2и т3. Движущие силы, создаваемые приводами в поступательных парах, равны соответственно F01, F12 и F23. Составить дифференциальные уравнения движения механизма. Трением пренебречь.
Решение.
Рассматриваемая механическая система имеет три степени свободы. Выберем обобщенные координаты: 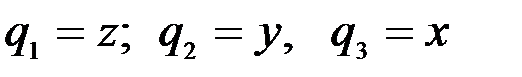 , тогда обобщенные скорости выразятся как
, тогда обобщенные скорости выразятся как 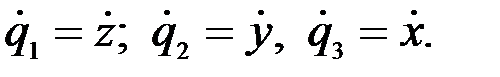
Вычислим кинетическую энергию системы. Т.к. звенья 1, 2 и 3 двигаются поступательно, то
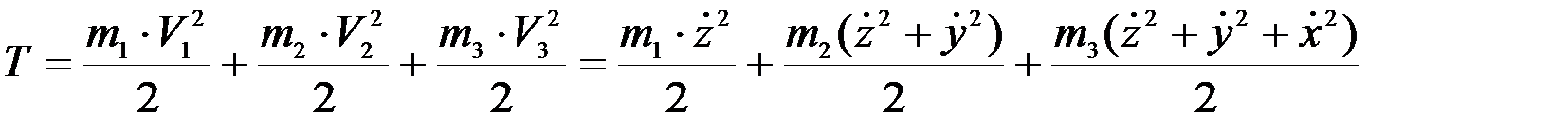 Вычислим частные производные от кинетической энергии:
Вычислим частные производные от кинетической энергии:
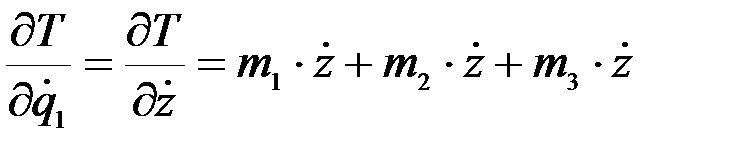 ;
;
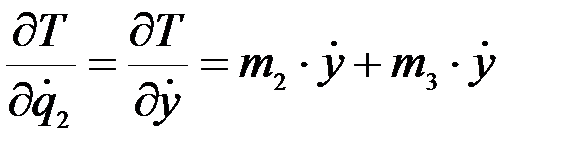 ;
;
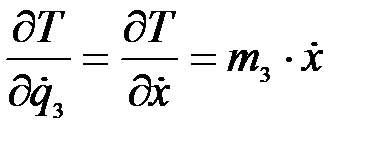 ,
,
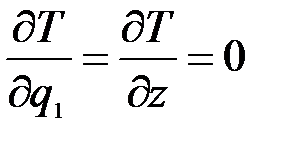 ;
; 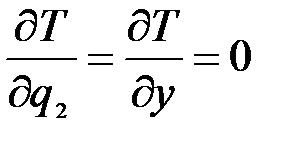 ;
; 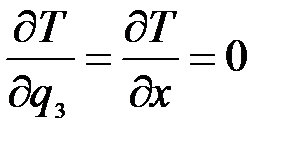 .
.
Далее, дифференцируя по времени, получим:
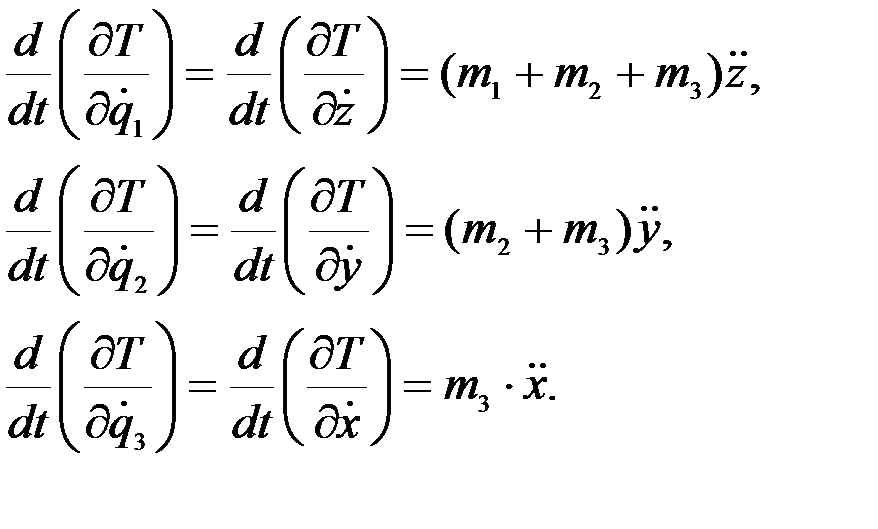
Для определения обобщенной силы 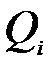 сообщим системе перемещение
сообщим системе перемещение 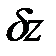 . При этом работу совершит движущая сила
. При этом работу совершит движущая сила 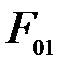 , направленная вверх, и силы тяжести всех 3-х звеньев:
, направленная вверх, и силы тяжести всех 3-х звеньев:
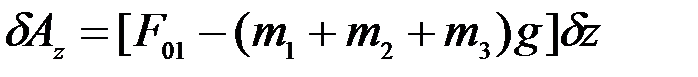 .
.
Многочлен, стоящий в квадратных скобках, является обобщенной силой: 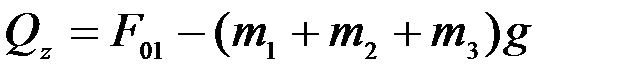 .
.
Аналогично вычислим обобщенные силы 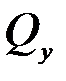 и
и 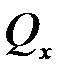 :
:
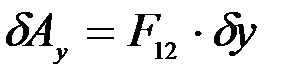 , тогда
, тогда 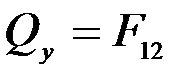 .
.
Силы тяжести не совершают работу, т.к. движение вдоль оси y происходит по горизонтали, поэтому
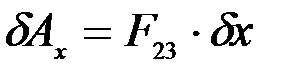 ,
,
откуда 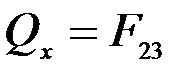 .
.
Запишем полученные дифференциальные уравнения движения:
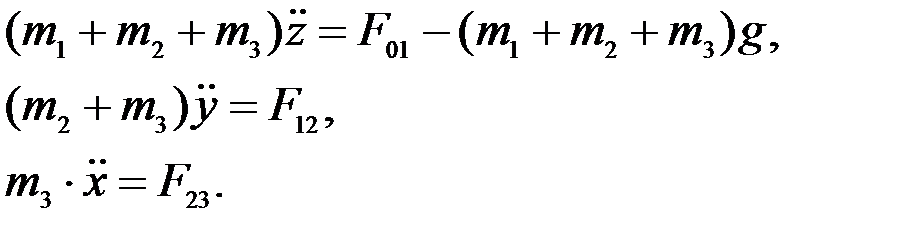
Дата добавления: 2015-12-26; просмотров: 1744;
