Принцип возможных перемещений
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю:
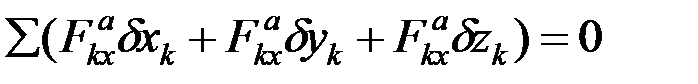 .
.
Этот принцип позволяет исключить из рассмотрения все заранее неизвестные реакции связей.
Равновесие рычага (золотое правило механики)
Представим рычаг, вращающийся на шарнире О, на концах которого действуют силы 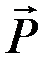 и
и  . Обозначим АО = а, ВО = в. Дадим системе возможное перемещение, тогда точки А и В сместятся соответственно на dQ и dP. Получим
. Обозначим АО = а, ВО = в. Дадим системе возможное перемещение, тогда точки А и В сместятся соответственно на dQ и dP. Получим 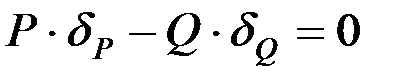 , а так как dQ = а·dj и dР = в·dj , то Ра·dj – Qв·dj = 0.
, а так как dQ = а·dj и dР = в·dj , то Ра·dj – Qв·dj = 0.
Сократив на dj,получим 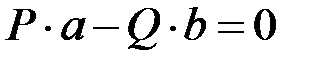 .
.
Это и есть условие равновесия рычага. Очевидно, что это уравнение моментов относительно точки О.
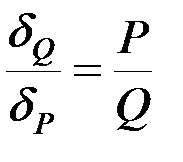 .
.
Если рычаг находится в равновесии под действием двух сил, то возможные перемещения точек приложения сил обратно пропорциональны этим силам. Это можно сформулировать так: то, что выигрывается в силе, теряется в скорости (золотое правило механики).
Принцип Даламбера–Лагранжа (общее уравнение динамики)
Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики при решении задач динамики. Следовательно, применение этих принципов одновременно позволит получить общий метод решения задач динамики.
Пусть дана система материальных точек А1, А2, ... Аn.
Если ко всем точкам системы, кроме действующих на них активных сил и реакций связей, приложить еще и силы инерции 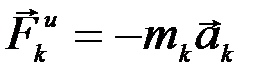 , то, согласно принципу Даламбера, система будет находится в равновесии. В соответствии с принципом возможных перемещений:
, то, согласно принципу Даламбера, система будет находится в равновесии. В соответствии с принципом возможных перемещений:
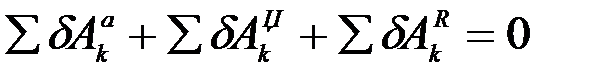 .
.
Если связи идеальные, то последняя сумма равна нулю, тогда:
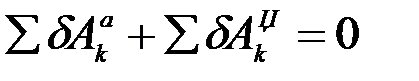 .
.
Это и есть принцип Даламбера–Лагранжа: при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.
Уравнение, выражающее этот принцип, называют общим уравнением динамики. В аналитической форме оно имеет вид:
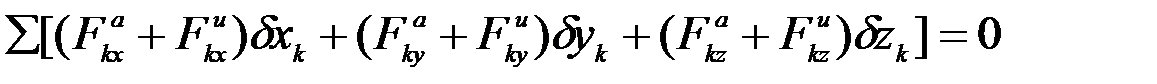 .
.
Если система представляет собой совокупность каких-нибудь твердых тел, то для составления уравнения нужно к действующим на каждое тело активным силам прибавить в любом центре силу, равную главному вектору сил инерции, и пару с моментом, равным главному моменту сил инерции относительно этого центра, а затем применить принцип возможных перемещений.
Пример.В подъемнике, изображенном на рисунке, к шестерне 1, имеющей массу m1 и радиус R1 , приложен вращающий момент М.  Определить ускорение поднимаемого груза 3 весом Q , пренебрегая весом веревки и трением в осях. Барабан, на который наматывается веревка, жестко скреплен с другой шестерней; их общая масса равна m2, радиус инерции равен i2, радиусы шестерен равны соответственно R1 и R2.
Определить ускорение поднимаемого груза 3 весом Q , пренебрегая весом веревки и трением в осях. Барабан, на который наматывается веревка, жестко скреплен с другой шестерней; их общая масса равна m2, радиус инерции равен i2, радиусы шестерен равны соответственно R1 и R2.
Решение.
Обозначим на рисунке все активные силы (в данном случае это силы тяжести тел) и применим к системе принцип Даламбера. Для этого приложим к грузу 3 силу инерции 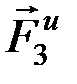 и к дискам 1 и 2 – моменты сил инерции
и к дискам 1 и 2 – моменты сил инерции 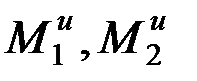 .
.
Теперь система находится в равновесии, и к ней можно применить принцип возможных перемещений (принцип Лагранжа). Для этого сообщим, например, грузу 3 возможное перемещение d3. Диски при этом получат перемещение dj1 и dj2 . Согласно принципу Даламбера–Лагранжа, сумма работ всех активных сил и всех сил инерции на возможном перемещении системы должна быть равна нулю. Следовательно,
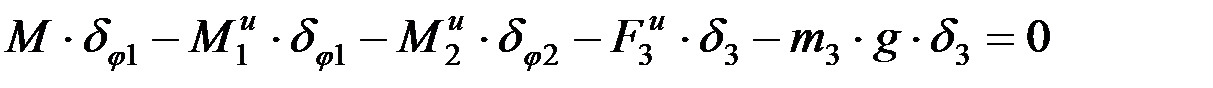 .
.
Выразим все перемещения через d3 . Для простоты решения задачи сначала выразим скорости всех тел через скорость груза 3. Т.к. связи дифференциальные и интегрируемые, перемещения и ускорения тел будут подвержены тем же зависимостям:
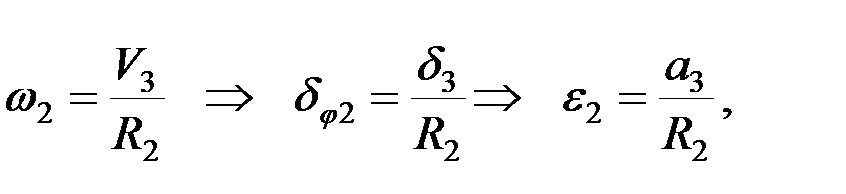
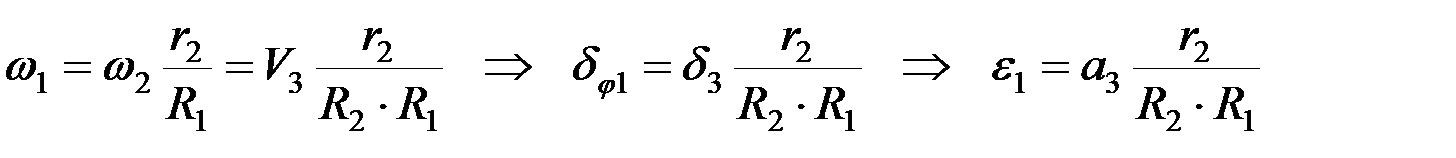 .
.
Далее выразим моменты и силы инерции с учетом уже полученных зависимостей:
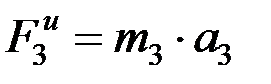 ;
;
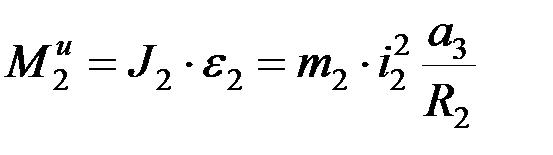 ;
;
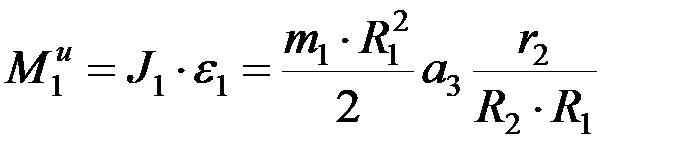 .
.
Подставим полученные значения в уравнение возможных работ. Далее, сократив левую и правую части уравнения на d3 , выразим a3.

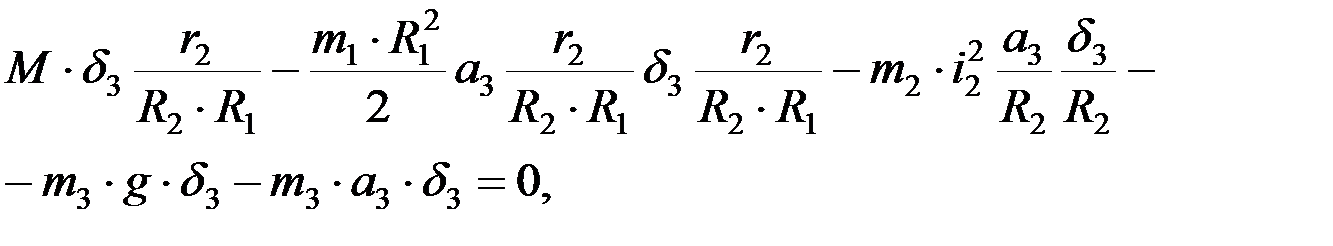
откуда 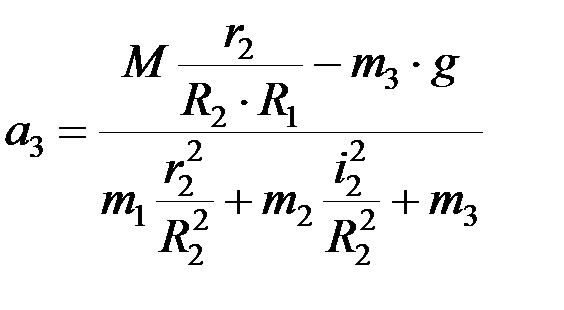 .
.
Дата добавления: 2015-12-26; просмотров: 933;
