СВЯЗИ. РЕАКЦИИ СВЯЗЕЙ

АКСИОМЫ СТАТИКИ

Статика изучает равновесие абсолютно твёрдого тела (АТТ). В её основе лежат простые положения, не требующие доказательств и являющиеся результатом обобщения опытных данных, наблюдений за поведением тел. Некоторые аксиомы являются простым следствием или непосредственно законами классической механики И. Ньютона.

Аксиома I (аксиома инерции, или первый закон Ньютона).

Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения, пока какие-нибудь силы не выведут тело из этого состояния.

Способность материального тела сохранять движение при отсутствии действующих сил или в постепенном изменении этого движения, когда на тело начинают действовать силы, называется инерцией. На основании этой аксиомы состоянием равновесия считаем такое состояние, когда тело находится в покое или движется прямолинейно и равномерно, т.е. по инерции.

Аксиома II.Для равновесия двух сил, приложенных к абсолютно твёрдому телу, необходимо и достаточно, чтобы эти силы были равны по модулю, действовали по одной прямой и направлены в противоположные стороны (рис. 2.1). Такие силы называют взаимоуравновешенными: ,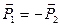

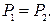
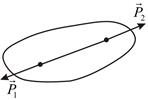
Рис. 2.1. Равные и противоположно направленные силы

Аксиома III (аксиома присоединения). Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней добавить (отнять) совокупность (систему) уравновешенных сил.

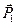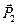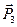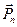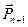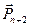Рассмотрим твёрдое тело (рис 2.2), находящееся под действием системы сил , , ,… . Прибавим еще две силы и , которые являются взаимно уравновешенными. Очевидно, что получилась новая система, эквивалентная данной.

Аналогичный результат получим при отбрасывании этих уравновешенных сил.

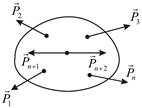
Рис. 2.2. Твёрдое тело под действием сил

Из второй и третьей аксиом вытекает как следствие следующее положение: механическое состояние абсолютно твёрдого тела не нарушится, если приложенную к нему силу переносить по линии ее действия в любую точку тела, иными словами, сила есть скользящий вектор.

Пусть на твёрдое тело действует сила 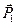в точке А по линии действия ав (рис. 2.3).

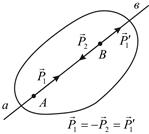
Рис. 2.3

В произвольной точке В на линии ав приложим две равные по модулю и противоположно направленные силы 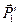и 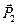. Согласно второй аксиоме силы 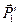и 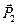взаимно уравновешены, а согласно третьей аксиоме их можно приложить к телу, не нарушая механического равновесия.

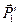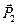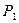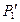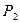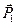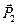Если силы и по модулю равны, то = = . Тогда силы и уравновешены, а оставшаяся сила 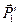заменяет силу 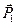, перенесённую из точки А в точку В по линии её действия. Механическое состояние тела не нарушается. Следствие доказано.

Аксиома IV (аксиома параллелограмма сил). Равнодействующая двух сил, приложенных к абсолютно твёрдому телу в одной точке под углом друг к другу, равна их геометрической сумме, т. е. выражается по модулю и направлению диагональю параллелограмма (рис. 2.4), построенного на этих силах. Точка приложения равнодействующей совпадает с точкой приложения данных сил: .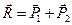

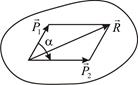
Рис. 2.4. Параллелограмм сил

Из аксиомы IV вытекает следствие (теорема о трёх силах): если три непараллельные силы, лежащие в одной плоскости, представляют собой уравновешенную систему, то линии действия этих сил пересекаются в одной точке.

Доказательство. Пусть к телу (рис. 2.5) в точках А, В и С приложены соответственно силы , , .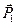

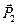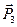Продолжим линии действия сил 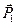и 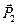до пересечения в точке О, перенесём в неё эти силы и найдём их равнодействующую 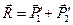. Равновесие тела при этом не нарушится, поэтому векторы силы 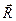и 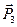должны быть равны по модулю, лежать на одной прямой и направлены в разные стороны. Следовательно, линия действия силы 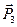также должна проходить через точку О, т.к. она совпадает с линией действия силы .

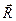Рис. 2.5. Равновесие тела под действием трёх сил

Аксиома V (аксиома взаимодействия). Силы взаимодействия двух тел между собой всегда равны по модулю и направлены по одной прямой в противоположные стороны.

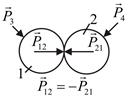
Рис. 2.6. Взаимодействие двух тел

Силы, которые действуют на систему тел со стороны других тел, не входящих в данную систему, называются внешними. Силы, с которыми отдельные тела системы действуют друг на друга, называются внутренними. На рис. 2.6 силы 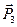, 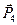– внешние, а 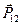, 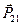– внутренние. В любой системе суммы внутренних сил всегда равны нулю.

Аксиома VI(аксиома отвердевания). Эта аксиома касается условий равновесия конструкции, испытывающей деформацию, или деформируемых частей сложной конструкции. Аксиома предполагает, что, если такая конструкция под действием системы сил находится в равновесии, её можно считать абсолютно твёрдой или отвердевшей. Анализ деформированного состояния рассматривается в курсе «Сопротивление материалов».

СВЯЗИ. РЕАКЦИИ СВЯЗЕЙ

Как показывает практика, любое приспособление, предмет, используемые человеком для облегчения физического труда, свободными быть не могут. Эти предметы обязательно вступают в связи (соприкосновения, опирания, закрепления и т.п.) с другими объектами. Такие объекты в теоретической механике называются связями. Связи представляют собой ограничения, налагаемые на положение и скорости точек механической системы; они противодействуют стремлению тела двигаться под действием активных сил. В соответствии с 3-им законом И. Ньютона со стороны связей к телу приложены силы, которые называются реакциями связей.

При решении задач статики активные силы, как правило, заданы, а реакции связей неизвестны, и их требуется определить. Определяя реакции связей, необходимо иметь в виду, что они приложены к телу в точках соприкосновения тела со связью и направлены в сторону, противоположную той, куда связь не дает перемещаться телу. Направление реакций связи зависит от вида связи, её расположения относительно тела и характера соприкосновения или соединения связи с телом.

Рассмотрим некоторые разновидности связей и правила определения их реакций.