Рівняння вузлових напруг

Матричне рівняння за методом вузлових напруг записується у вигляді

, ( )

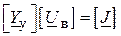де 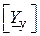- квадратна матриця вузлових провідностей.

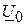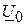Задача знаходження напруг при заданих струмах у вузлах мережі має єдиний розв’язок в тому випадку, коли в одному з вузлів напруга задана. В якості такого базисного вузла зазвичай приймають балансуючий. Напруга в ньому позначається . Напруги решти вузлів доцільно визначати відносно базисної величини як спад напруги від кожного з незалежних вузлів схеми до базисного

, ( )

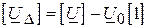де 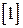- одинична матриця.

Для вирішення поставленої задачі необхідно визначити вектор через вектор 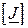задаючих струмів. Задаючі струми 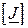пов’язані зі струмами віток 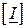першим законом Кірхгофа (див. формулу ( )); в свою чергу вектор 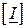визначає спад напруги у вітках (див. формулу ( )). Отже, визначимо вектор 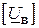через шуканий вектор .

Залежність 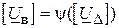легко знайти, використовуючи транспоновану матрицю 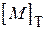. Для цього досить помножити її справа на стовпець спадів напруг , щоб знайти стовпець різниці напруг на кінцях кожної вітки:

. ( )

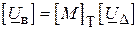Щоб зв’язати шуканий вектор зі струмами віток, в рівняння ( ) підставимо вираз 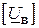, отриманий раніше (див. формулу ( )),

, звідки

.

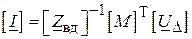І, нарешті, підставляючи цей вираз у формулу ( ), отримаємо шукану залежність між задаючими струмами 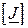та шуканими спадами напруг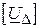

. ( )

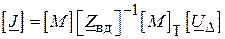Для спрощення отриманого рівняння визначимо матрицю провідностей віток як та позначимо

. ( )

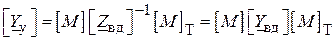Квадратна матриця ( ) порядку n–1 називається матрицею вузлових провідностей. Вона й дає кінцеву форму запису ( ) вузлових рівнянь

. ( )

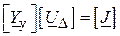Матриця 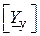симетрична, оскільки 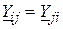. Для розглядуваної схеми вона має вигляд

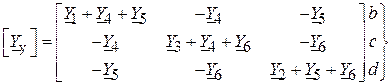вузли,

b c d вузли.

Важливою особливістю матриці 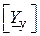є її дуже мала наповненість – більшість недіагональних елементів дорівнюють нулю, оскільки кожен з вузлів зв’язаний вітками лише з кількома найближчими (схема на рис. 9.3 в цьому відношенні нехарактерна). Ця властивість відіграє вирішальну роль у спрощенні обчислюваної процедури при розв’язанні системи рівнянь ( ).