Матричний метод розрахунку складно-замкнених мереж

Матрицею являється таблиця величин, що мають спільні ознаки і записані у визначеній послідовності. Для цього всі величини , які входять у цю таблицю, повинні бути відповідно пронумеровані.

Алгебра матриць дозволяє одночасно оперувати цілими групами величин і записувати дії над ними спрощено – через символи. Перевагами матриць є компактність, відсутність громіздких записів та стислість. Тобто є можливість більшої наочності математичних формулювань і перетворень.

Якщо детально записати системи лінійних рівнянь ( ) і ( ), то вони матимуть наступний загальний вигляд:

( )

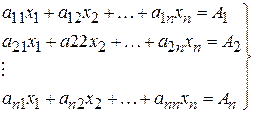В цю систему рівнянь входять три групи комплексних величин: відшукувані величини 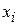, вільні члени 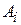та коефіцієнти 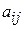при невідомих. Індекси мають значення 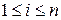; ; 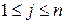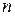– число рівнянь.

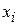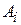Кожну з груп величин та можна записати у вигляді таблиці, яка буде складатися з одного стовпця

; ,

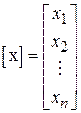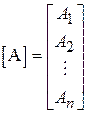тобто у вигляді стовпцевої матриці.

Трохи в іншій формі записується таблиця коефіцієнтів 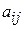, оскільки вони мають два індекси 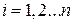та .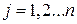

Відповідна таблиця повинна мати ж стільки рядків, скільки й стовпців, тобто вона – квадратна:

. ( )

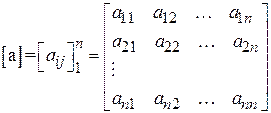Число 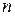показує порядок таблиці, який відповідає числу рівнянь.

Таким чином, матриці струмів та напруг (ЕРС) є стовпцевими, а матриці опорів і провідностей – квадратними.

Матриця провідностей:

. ( )

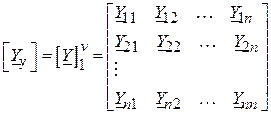Коефіцієнти з однаковими індексами (сумарні провідності віток, з’єднаних з відповідним вузлом) розташовуються по діагоналі матриці, яка називається головною діагоналлю. На перетині рядка 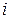та стовпця 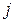розташовується провідність вітки, що з’єднує вузли 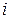та 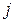, яка береться зі зворотним знаком.

Для схеми, що має властивість взаємності, 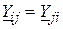, тобто матриця 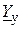– симетрична відносно головної діагоналі.

Матриця опорів:

. ( )

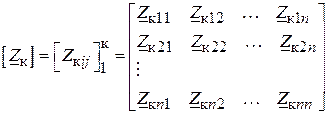По головній діагоналі цієї матриці розташовуються власні опори відповідних контурів, а на перетині рядка 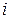та стовпця 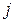– суміжні опори контурів 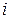та 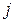. Якщо напрямки контурних струмів 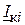і 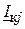у відповідній вітці схеми співпадають, то опір записується з позитивним знаком, а якщо струми мають протилежний напрямок, то опір записується з від’ємним знаком.

Квадратна матриця 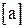володіє особливими властивостями, якщо її визначник 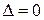. Така матриця називається особливою.

Якщо визначник 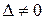, то матриця неособлива. Особливою також є матриця, сума елементів якої кожного стовпця або кожного рядка рівна нулю.

Якщо кожній вітці задати певний напрям, то отримаємо схему, що називають спрямованим графом. Останній характеризує конфігурацію мережі, будову схеми, встановлює взаємний зв’язок віток та вузлів. Схемі рис. 9.3 відповідає граф рис. 9.4.

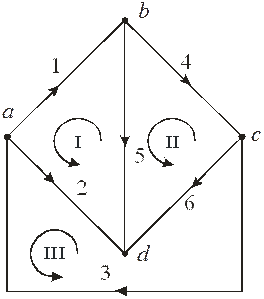
Рисунок 9.4. Спрямований (орієнтовний) граф мережі

Спрямований граф описують за допомогою двох матриць, що називають першою та другою матрицями з’єднань, або інциденцій. Перша характеризує з’єднання у вузлах (матриця ).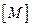

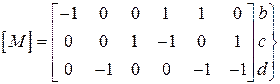вузли, ( )

1 2 3 4 5 6 – вітки.

Кожен рядок 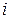цієї матриці відповідає визначеному незалежному вузлу схеми, а кожен стовпець 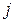– вітці схеми. На перетині рядка 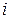та стовпця 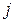записується +1, якщо вітка 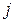з’єднана з вузлом 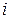своєю початковою вершиною, тобто має напрямок від вузла 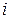; –1 записується, коли вітка 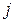спрямована до вузла 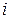, тобто з’єднана з ним кінцевою вершиною; 0 записується, коли вітка 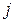не з’єднана з вузлом .

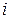У кожному рядку матриці 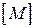повинно бути не менше однієї позитивної або від’ємної одиниці. В противному разі даний вузол не матиме з’єднання з іншою частиною схеми. Число +1 показує, скільки віток з’єднано з даним вузлом своїми початковими вершинами. Число –1 показує кілікість віток, з’єднаних з цим вузлом кінцевими вершинами.

Сумарна кількість одиниць (і +1, і – 1) в кожному рядку показує число віток, з’єднаних з даним вузлом 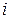того ж номера.

У кожному стовпці матриці 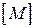може бути тільки одна +1 або –1. Сумарне число одиниць може бути від однієї до двох. Ці одиниці показують початкові і кінцеві вершини даної вітки. Якщо у стовпці тільки одна 1, то це означає, що другою вершиною дана вітка з’єднується з базисним вузлом.

Матриця 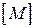– прямокутна. Вона повинна мати стільки рядків, скільки схема має незалежних вузлів, і стільки стовпців, скільки у схемі віток. Сумарна кількість одиниць у ній рівна сумарному числу вершин віток, з’єднаних з незалежними вузлами схеми.

Друга 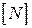називається матрицею з’єднань у контурах

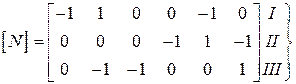контури, ( )

1 2 3 4 5 6 – вітки.

В матриці 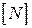на перетині рядка 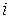та стовпця 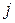записується +1, якщо вітка 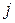входить до контуру 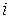та має напрямок, що співпадає з напрямком контуру; –1, якщо вітка 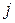входить до контуру 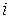, але має напрямок, протилежний напрямку обходу контуру; 0, коли вітка 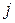не входить до контуру .

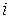Другу матрицю інциденцій 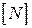можна скласти безпосередньо за схемою з’єднань, якщо вибрати незалежні контури, напрямки їх обходу і напрямки всіх віток.

Рівняння стану електричного кола в матричній формі (рівняння першого закону Кірхгофа):

, ( )

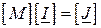де 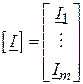– вектор-стовпець (стовпцева матриця) струмів у вітках;

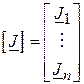– вектор-стовпець задаючих струмів у вузлах.

Систему взаємно незалежних рівнянь за другим законом Кірхгофа можна записати у вигляді:

, ( )

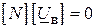де 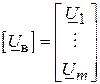– вектор-стовпець напруги у вітках схеми.

Скориставшись законом Ома, запишемо

, ( )

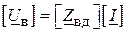де 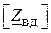– діагональна матриця комплексних опорів віток

Отже, з рівнянь ( ) та ( ) отримаємо матричне рівняння за другим законом Кірхгофа

. ( )

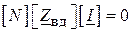Узагальнене рівняння стану електричного кола (система рівнянь)

, . ( )

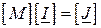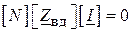Ці рівняння можна об’єднати в одне, вводячи об’єднану матрицю параметрів заступної схеми мережі

. ( )

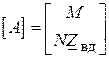Тепер узагальнене рівняння стану приймає компактний вигляд

. ( )

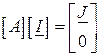Матриця 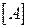є квадратною і неособливою, тому рівняння (8) можна розв’язати відносно шуканих струмів

. ( )

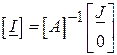Елементи оберненої матриці знаходяться за допомогою виразу

,

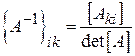де 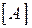- алгебраїчне доповнення елемента 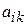у визначнику .

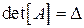Для запису узагальненого рівняння (для схеми рис. 9.3) попередньо запишемо матрицю :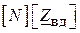

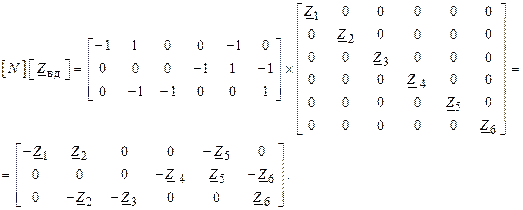
Тоді рівняння (8) у розгорнутому вигляді буде записане так

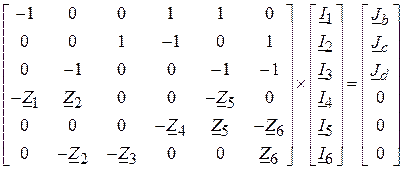
Це так званий прямий метод розрахунку.

До раціональних методів розрахунку складно-замкнених мереж відносяться метод контурних струмів та метод вузлових напруг.