Рівняння стану електричного кола

До розрахунку електричних мереж застосовні закони Ома та Кірхгофа, а також відомі методи розрахунку електричних кіл.

Будь-який усталений режим роботи електричної системи описується системою лінійних алгебраїчних рівнянь. В якості відшукуваних величин можуть бути струми у вітках або напруги між вузлами.

В теорії електричних кіл вузлом називається точка схеми, до якої приєднано більше двох віток. Однак, при розрахунках режимів роботи електричних мереж доцільно у поняття “вузол” включати точки, у яких з’єднується і менша кількість віток, або точка прикладення задаючого струму (якщо, наприклад, у цих точках необхідна фіксація напруги).

Алгебраїчні рівняння (системи рівнянь), які визначають робочий режим електричної системи, називаються рівняннями стану. Найчастіше при розрахунках робочих режимів електричної системи (ЕС) застосовуються вузлові або контурні рівняння.

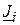Задача формулюється так: задана конфігурація мережі (її топологія); опори , схеми заміщення її віток; навантаження вузлів у вигляді струмів або потужностей 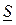. Треба визначити напруги 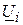у вузлах схеми, перш за все у вузлах з навантаженням.

Напруга у вузлах мережі повністю визначається струмами її віток. Ці струми залежать від задаючих вузлових струмів 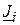, параметрів елементів схеми та її конфігурації. Взаємний зв’язок між переліченими величинами описується рівняннями стану кола (за допомогою законів Ома та Кірхгофа).

В схемі (рис. 9.3) 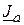– струм живлячого джерела; 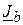, , 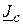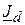– струми навантажень. Задаємо довільні напрями струмів у вітках і напрями обходу контурів.

Рівняння за першим законом Кірхгофа складається для n–1 вузлів:

( )

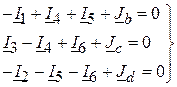Умова балансу струмів будь-якого кола:

.

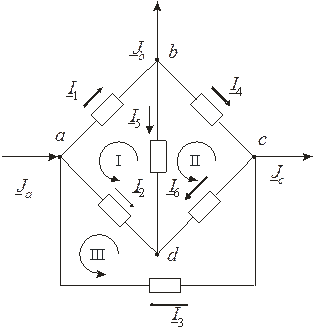
Рисунок 9.3. Заступна схема багатоконтурного електричного кола

Вузол, що відповідає виключеному рівнянню, називають вузлом балансу, або балансуючим вузлом. Для схеми, що має m віток, n вузлів, кількість незалежних контурів: 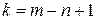. Для них рівняння за другим законом Кірхгофа:

, ( )

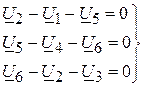де 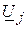– спад напруги у вітках схеми.

Використовуючи закон Ома, перепишемо рівняння ( ) у вигляді

. ( )

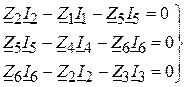Вузлове рівняння для будь-якого незалежного вузла має наступний вигляд:

, ( )

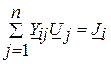де 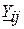– комплексне значення провідності;

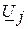– комплексне значення напруги між 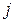вузлом схеми і базисним вузлом;

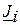– комплексне значення задаючого струму у вузлі і схеми. (За позитивний напрямок прийнятий напрямок до вузла схеми). При відсутності задаючих струмів у вузлах схеми контурне рівняння для будь-якого незалежного контуру має вигляд:

. ( )

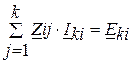Система ( ),( ) достатня для визначення струмів у всіх вітках схеми. Для застосування ЕОМ слід максимально формалізувати всі етапи розрахунку, отримати чіткі алгоритми, для чого зручно скористатись алгеброю матриць та положеннями теорії графів.