Узагальнене зображення схем та рівнянь електричних мереж
При узагальненому записі рівнянь:
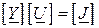 ( )
( )
з’являється можливість узагальненого зображення схем. Замість позначення на схемі окремих величин (опорів, ЕРС, струмів) можна користуватись умовними позначеннями цілих груп величин, які входять у відповідні матриці. Таке зображення дозволяє спростити принципову постановку задачі та її розв’язок. Наприклад, для рівняння ( ) можна зобразити наступну схему:
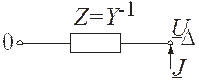
Рисунок 9.6. Узагальнена схема електричної мережі
Тут у вигляді одного незалежного вузла представлені всі 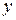 незалежних вузлів, матрицею
незалежних вузлів, матрицею 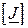 представлені всі задаючі струми, прикладені до цих вузлів; матрицею
представлені всі задаючі струми, прикладені до цих вузлів; матрицею 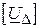 – позначені спади напруг між цими вузлами і вузлом балансу, матрицею
– позначені спади напруг між цими вузлами і вузлом балансу, матрицею 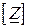 визначені всі вузлові опори.
визначені всі вузлові опори.
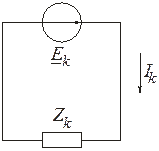
Рисунок 9.7. Контурна узагальнена схема
На рис. 9.7 представлена схема у вигляді одного контуру. На ній показані матрицями всі характерні величини – контурні опори 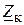 , контурні ЕРС
, контурні ЕРС 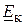 і контурні струми
і контурні струми 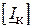 . Тут в позначення контурних опорів входять не тільки власні опори контурів, але і загальні для них опори у відповідності з рівнянням:
. Тут в позначення контурних опорів входять не тільки власні опори контурів, але і загальні для них опори у відповідності з рівнянням:
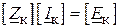 . ( )
. ( )
Узагальнене представлення схем застосовується для наочності постановки задачі. Фактична схема з’єднань при цьому залишається невідомою. Але для вирішення конкретних завдань вона повинна враховуватись. Для вирішення практичних задач необхідно відображати характер з’єднання віток схеми двояким чином: у вузлах і в незалежних контурах. Для характеристики конкретної схеми з’єднань віток і застосовують матриці інциденцій (з’єднань).
Важливим є погодження позитивних напрямків для всіх використовуваних в розрахунках величин. Оскільки позитивні напрямки потрібні не тільки для визначення струмів у вітках, але й ЕРС та напруг, то доцільно відносити їх до кожної вітки схеми. Позитивні напрямки є умовними і приймаються довільно.
Рівняння Кірхгофа в узагальненій формі для будь-якого вузла 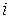 схеми (перше рівняння стану електричної системи) має наступний вигляд:
схеми (перше рівняння стану електричної системи) має наступний вигляд:
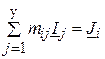 , ( )
, ( )
де 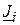 – комплексне значення задаючого струму у вузлі
– комплексне значення задаючого струму у вузлі 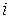 ;
;
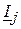 – комплексне значення струму у вітці
– комплексне значення струму у вітці 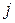 ;
;
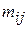 – коефіцієнт матриці з’єднань.
– коефіцієнт матриці з’єднань.
Коефіцієнти 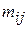 можуть приймати тільки одне з трьох значень: +1; –1; 0.
можуть приймати тільки одне з трьох значень: +1; –1; 0.
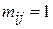 , якщо струм
, якщо струм 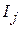 по вітці
по вітці 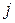 має напрямок від вузла
має напрямок від вузла 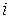 .
.
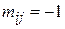 , якщо струм
, якщо струм 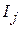 по вітці
по вітці 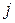 має напрямок до вузла
має напрямок до вузла 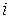 .
.
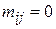 , якщо вітка
, якщо вітка 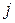 не з’єднана з вузлом
не з’єднана з вузлом 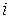 , тобто струм
, тобто струм 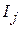 не входить у рівняння балансу для вузла і схеми.
не входить у рівняння балансу для вузла і схеми.
Рівняння ( ) можна записати у матричному вигляді (див. рівняння ( )).
Матриця 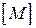 відображає з’єднання віток у вузлах схеми.
відображає з’єднання віток у вузлах схеми.
Матриця 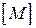 широко застосовується для визначення співвідношень між вузловими величинами. Вона дозволяє визначити матрицю
широко застосовується для визначення співвідношень між вузловими величинами. Вона дозволяє визначити матрицю 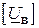 спадів напруги у вітках схеми (між початковими і кінцевими вершинами) по відомій матриці
спадів напруги у вітках схеми (між початковими і кінцевими вершинами) по відомій матриці 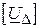 спадів напруги між кожним незалежним вузлом схеми і її базисним вузлом
спадів напруги між кожним незалежним вузлом схеми і її базисним вузлом
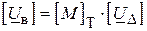 , ( )
, ( )
де 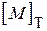 – транспонована матриця
– транспонована матриця 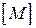 .
.
Аналогічно ( ) рівняння другого закону Кірхгофа (друге рівняння стану) для кожного із незалежних контурів має наступний вигляд:
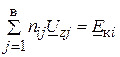 , ( )
, ( )
де 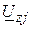 – комплексне значення спаду напруги на опорі
– комплексне значення спаду напруги на опорі 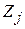 вітки
вітки 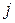 ;
;
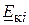 – комплексне значення контурної ЕРС, тобто сумарної ЕРС для контуру
– комплексне значення контурної ЕРС, тобто сумарної ЕРС для контуру 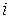 ;
;
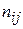 – коефіцієнт (має три значення: +1; –1; 0).
– коефіцієнт (має три значення: +1; –1; 0).
Ці коефіцієнти визначаються:
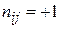 , якщо напрямок струму по вітці
, якщо напрямок струму по вітці 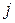 , що входить до контуру
, що входить до контуру 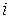 , співпадає з напрямком обходу цього контуру;
, співпадає з напрямком обходу цього контуру;
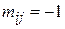 , якщо напрямки протилежні;
, якщо напрямки протилежні;
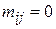 , якщо вітка
, якщо вітка 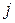 не входить у контур
не входить у контур 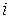 .
.
Рівняння ( ) можна записати у матричній формі:
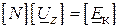 . ( )
. ( )
Тут матриця 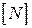 визначає з’єднання віток у незалежні замкнуті контури – друга матриця інциденцій.
визначає з’єднання віток у незалежні замкнуті контури – друга матриця інциденцій.
Відзначимо, що матриці 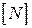 і
і 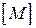 відображують тільки електричні зв’язки. Наявність магнітних зв’язків в них не відображається.
відображують тільки електричні зв’язки. Наявність магнітних зв’язків в них не відображається.
Матриця 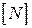 застосовується при визначенні співвідношень між контурними величинами.
застосовується при визначенні співвідношень між контурними величинами.
Вона дозволяє визначити контурні ЕРС схеми, якщо відомі ЕРС віток. Це записується наступним чином
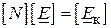 . ( )
. ( )
При перемноженні матриці 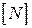 на матрицю
на матрицю 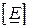 отримуємо алгебраїчну суму ЕРС у всіх вітках даного контуру.
отримуємо алгебраїчну суму ЕРС у всіх вітках даного контуру.
Із рівнянь ( ) і ( ) при відсутності в схемі ЕРС отримуємо:
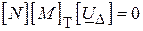 . ( )
. ( )
Оскільки сумарні спади напруги на всіх вітках, які входять до кожного незалежного контуру системи, повинні рівнятись нулю, то
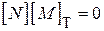 . ( )
. ( )
Якщо у рівняння ( ) підставити вираз матриць 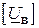 і
і 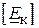 :
: 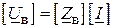 та
та 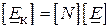 , то отримаємо друге рівняння стану електричної системи у більш детальній матричній формі:
, то отримаємо друге рівняння стану електричної системи у більш детальній матричній формі:
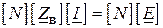 ( )
( )
або
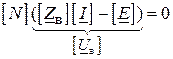 , тобто
, тобто 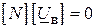 ( )
( )
тут 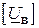 – матриця спадів напруги у вітках схеми.
– матриця спадів напруги у вітках схеми.
При наявності ЕРС у вітках:
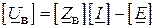 . ( )
. ( )
Рівняння ( ) є виразом для закону Ома у матричній формі
Приклад .
Розглянемо граф електричної схеми зображеної на рис. 9.8.
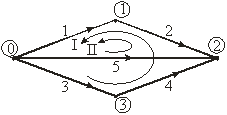
Рисунок 9.8. Орієнтований граф для визначення другої матриці інциденцій
На приведеній схемі показані номери і напрямки усіх віток та номери вузлів. Число незалежних контурів
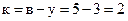 .
.
В контур І входять вітки 3, 4, 2, 1, причому напрямки віток 3 і 4 співпадають з напрямком обходу контуру, а напрямки віток 2 і 1 – протилежні йому. Вітка 5 не входить в контур 1, тому для першого рядка можна записати: –1 –1 1 1 0. Аналогічно для другого рядка (другого контуру)
–1 –1 0 0 1
Тоді матриця 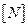 матиме вигляд
матиме вигляд
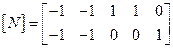 .
.
Кожний стовпець 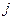 матриці
матриці 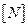 відповідає вітці
відповідає вітці 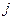 схеми і показує, в які контури входить ця вітка і з яким напрямком. Кожний рядок
схеми і показує, в які контури входить ця вітка і з яким напрямком. Кожний рядок 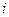 цієї матриці показує, з яких віток складається даний контур.
цієї матриці показує, з яких віток складається даний контур.
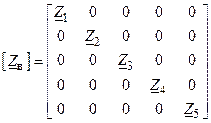 .
.
На рис. 9.9 показана відповідна узагальнена схема електричної системи. Тут всі параметри визначені матрицями.
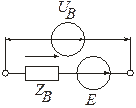
Рисунок 9.9. Узагальнена схема електричної системи
Дерево схеми. Найменша частина замкнутої схеми, вітки якої з’єднують точку балансу з іншими її вузлами, називають деревом схеми. Число віток, які входять до дерева схеми, рівне числу незалежних вузлів. Дерево можна вважати основною частиною (скелетом) схеми (рис. 9.10).
Доцільно так складати матрицю 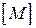 , щоб перші її стовпці відповідали віткам дерева схеми. Наприклад, у схеми рис. 9.7 є три незалежні вузла, тому в дерево повинні входити лише три вітки, ще не утворюють замкнутого контуру, – наприклад, 1, 2 і 3 (рис. 9.10,б).
, щоб перші її стовпці відповідали віткам дерева схеми. Наприклад, у схеми рис. 9.7 є три незалежні вузла, тому в дерево повинні входити лише три вітки, ще не утворюють замкнутого контуру, – наприклад, 1, 2 і 3 (рис. 9.10,б).
Якщо ці три стовпці записати у вигляді матриці окремо, то нова матриця 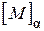 буде квадратною (індекс
буде квадратною (індекс 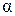 показує, що матриця відноситься до дерева схеми). Порядок матриці
показує, що матриця відноситься до дерева схеми). Порядок матриці 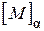 , рівний числу віток, які входять до дерева схеми:
, рівний числу віток, які входять до дерева схеми:
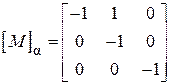 .
.
Ця матриця є першою матрицею інцинденцій для схеми, яка складається тільки з одного дерева.
Із однієї й тієї ж замкнутої схеми можна виділити декілька дерев. Вони відрізнятимуться лише складом віток схеми, що входять до них.
а) б)
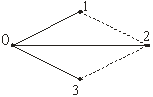
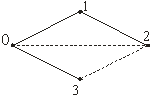
Рисунок 9.10. Дерева графа (суцільні лінії) і хорди (штрихові лінії)
Хорди (з’єднання). Вітки замкнутої схеми, які не входять до складу дерева називаються хордами (з’єднаннями).
Якщо після нумерації віток дерева схеми інші вітки (хорди) позначити наступними номерами, то легко матрицю 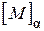 доповнити матрицею
доповнити матрицею 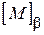 до матриці
до матриці 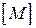 . Для цього в кожному черговому стовпці, номер якого рівний номеру відповідної хорди, «+1» записують у рядку, що відповідає номеру початкової вершини цієї вітки, а «–1» – у рядку, що відповідає номеру її кінцевої вершини.
. Для цього в кожному черговому стовпці, номер якого рівний номеру відповідної хорди, «+1» записують у рядку, що відповідає номеру початкової вершини цієї вітки, а «–1» – у рядку, що відповідає номеру її кінцевої вершини.
Для схеми рис. 9.10,б матриця 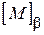 має вигляд:
має вигляд:
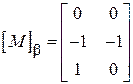 . ( )
. ( )
Оскільки число віток у будь-якій схемі рівне сумі числа незалежних вузлів і числа незалежних контурів 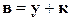 , то число хорд завжди рівне числу незалежних контурів
, то число хорд завжди рівне числу незалежних контурів 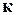 схеми. Очевидно, що додавання хорд створює незалежний контур. Тому доцільно так вибирати незалежний контур, щоб кожна з хорд входила тільки в який-небудь один незалежний контур.
схеми. Очевидно, що додавання хорд створює незалежний контур. Тому доцільно так вибирати незалежний контур, щоб кожна з хорд входила тільки в який-небудь один незалежний контур.
Раніше рівняння стану електричної системи були записані окремо ( ) та ( ):
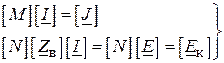 ( )
( )
Ці рівняння, на загал, називаються повними рівняннями Кірхгофа.
Неважко побачити, що матриці 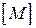 і
і 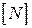 мають однакову кількість стовпців, рівну числу віток схеми, але різну кількість рядків, рівну, відповідно, числу незалежних вузлів і числу незалежних контурів. Звідки слідує, що об’єднавши матриці
мають однакову кількість стовпців, рівну числу віток схеми, але різну кількість рядків, рівну, відповідно, числу незалежних вузлів і числу незалежних контурів. Звідки слідує, що об’єднавши матриці 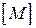 та
та 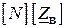 отримаємо квадратну неособливу матрицю:
отримаємо квадратну неособливу матрицю:
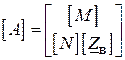 . ( )
. ( )
Об’єднавши матричні рівняння ( ), отримаємо необхідний вираз:
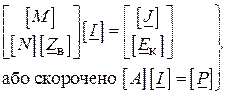 , ( )
, ( )
де: 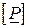 – блокова матриця активних параметрів схеми.
– блокова матриця активних параметрів схеми.
Запис рівняння стану в узагальненому вигляді ( ) дає можливість отримати розв’язок:
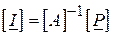 . ( )
. ( )
Відомо, що для визначення робочого режиму складної схеми немає потреби в спільному розв’язанні системи рівнянь ( ). Наприклад, метод контурних струмів приводить до необхідності вирішення тільки 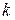 рівнянь, які є контурними, а метод вузлових потенціалів приводить до спільного вирішення
рівнянь, які є контурними, а метод вузлових потенціалів приводить до спільного вирішення 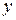 рівнянь, які є вузловими. Для скорочення числа спільно розв’язуваних рівнянь застосовується наступне.
рівнянь, які є вузловими. Для скорочення числа спільно розв’язуваних рівнянь застосовується наступне.
Недоцільно визначати струми усіх 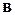 віток. Схеми шляхом спільного розв’язку
віток. Схеми шляхом спільного розв’язку 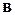 рівнянь, оскільки не всі струми є незалежними, якщо струми у вузлах відомі.
рівнянь, оскільки не всі струми є незалежними, якщо струми у вузлах відомі.
Розділивши рівняння ( ) на блоки
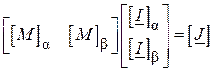 . ( )
. ( )
і, виконавши операції множення, отримаємо
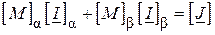 , ( )
, ( )
звідки
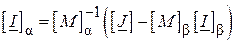 ,
,
або
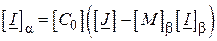 , ( )
, ( )
де 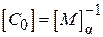 .
.
Приклад. Дана схема електричної мережі (рис 9.11).
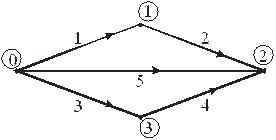
Рисунок 9.11. Схема (граф) електричної мережі
Задані струми у вітках 5, 4, які прийняті в якості хорд,
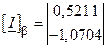
Схему рис. 9.11 можна спростити, подавши її у вигляді дерева:
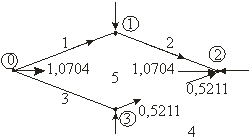
Рисунок 9.12. Дерево графа, зображеного на рис. 9.11
Тепер струми в усіх інших вітках знаходяться безпосередньо
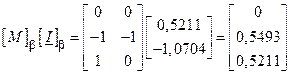
Ці струми складаються з задаючими струмами схеми:
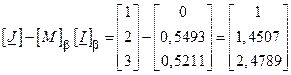 .
.
Тоді, перемноживши на 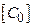 отримаємо:
отримаємо:
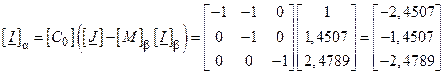 .
.
Висновок: струми у вітках дерева залежать від струмів у хордах. Тобто, незалежними для будь-якої схеми є тільки струми в хордах.
Незалежні спади напруги у вітках схеми, знаходимо, якщо у рівнянні ( ) розділити матриці на блоки:
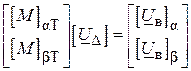 , ( )
, ( )
звідки
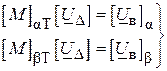 , ( )
, ( )
або
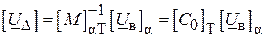 ; ( )
; ( )
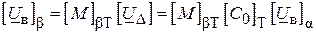 . ( )
. ( )
Це означає, що достатньо знати спад напруги на вітках дерева схеми, щоб визначити напруги на інших вітках, тобто хордах. Очевидно, що робочий режим будь-якої схеми повністю визначається значенням падінь напруги, що входять в матрицю 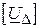 .
.
Дата добавления: 2015-12-22; просмотров: 2307;
